கருந்துளைகள் பற்றி விரிவான விளக்கம்

 

பூமியில் இருந்து ஒரு விண்கலம் பூமியின் ஈர்ப்பு விசையை விட்டு விண்வெளியை அடையவேண்டுமெனில் அது ஒரு செக்கனுக்கு 11.2 கிலோமீட்டர் வேகத்தில் பயணிக்கவேண்டும். அவ்வாறானா வேகத்தில் பயணித்தே நமது விண்கலங்கள் விண்வெளியை அடைகின்றது.

ஒரு கல்லை எடுத்து, வான் நோக்கி வீசி எறிந்தால், அக்கல் சிறிது தூரம் மேலெழும்பி, மீண்டும் கீழே விழுந்துவிடும். நாம் எறியும் வேகத்தைப் பொறுத்து அது மேலெழும்பும் தூரம் வேறுபடும். ஆக நீங்கள் எறியும் கல் மீண்டும் திரும்பி விழாமல் இருக்க வேண்டும் என்றால் நீங்கள் அதை ஒரு செக்கனுக்கு 11.2 கிலோமீட்டர் வேகத்தில் பயணிக்குமாறு எறியவேண்டும். இவ் வேகமானது விடுபடு திசைவேகம் (escape velocity) என அழைக்கப்படும்.

கோள்களின் திணிவுக்கு ஏற்ப அவற்றின் விடுபடு திசைவேகம் மாறுபடும், உதாரணமாக நமது சந்திரனின் விடுபடு திசைவேகம் செக்கனுக்கு 2.4 கிலோமீட்டர் ஆகும். இதையே சூரியனது விடுபடு திசைவேகத்தோடு ஒப்பிட்டுப் பார்த்தல், அதன் விடுபடு திசைவேகமானது ஒரு செக்கனுக்கு 617.5 கிலோமீட்டர் ஆகும்.

ஜான் மிச்சல் என்ற ஆசாமி 1783 இல் ஹென்றி காவன்டிஷ் என்ற ராயல் சொசைட்டி பௌதீகவியலாலருக்கு ஒரு கடிதம் எழுதினார். அதில் அவர் ஒரு விண்மீனின் விடுபடு திசைவேகம் ஒளியின் வேகத்தை விட அதிகமாக, அதாவது, ஒரு செக்கனுக்கு 300,000 கிலோமீட்டரை விட அதிகமாக இருந்தால், அந்த விண்மீனால் வெளிவிடப்படும் ஒளியானது மீண்டும் அதே விண்மீனால் இழுத்து உள்வாங்கப்பட்டுவிடுமா என்பது போன்ற ஒரு கேள்வியை கேட்டிருந்தார்.

கருந்துளை (படம் இணையம்)

இது ஒரு இக்கட்டான நிலையை உருவாக்கிவிட்டது, 1800களில் ஒளியைப் பற்றி நாம் தெரிந்திருந்தது சொற்பமே, அதிலும் ஒளியானது அலைவடிவமாக கருதப்பட்டதனால், ஈர்ப்புவிசை எவ்வாறு ஒளியில் தாக்கம் செலுத்தும் என்பது ஒரு புரியாத புதிராகேவே இருந்தது எனலாம். இதனாலோ என்னவோ, இந்த புரியாத கருப்பு விண்மீன்கள் பற்றி பெரிதாக அவர்கள் சிந்திக்கவில்லை.

இருபதாம் நூற்றாண்டின் தலைசிறந்த பௌதீகவியலாலரான அல்பர்ட் ஐன்ஸ்டீன், தனது பொதுச்சார்புக் கோட்பாடு (general relativity) மூலம் பெரும் விஞ்ஞானப் புரட்சியையே நிகழ்த்தினார். இக்கோட்பாடுகளில் ஒளியின் தன்மை பற்றிய புதிய கோட்பாடுகள், ஈர்ப்பு விசை எவ்வாறு ஒளியின் தன்மையில் செல்வாக்கு செலுத்தும் என்பது போன்ற கருத்துக்களும் அடங்கும்.

ஐன்ஸ்டீன் 1915 இல் பொதுச்சார்புக் கோட்பாட்டை வெளியிட்டு சிலமாதங்களில், கணிதவியலாளரான கார்ல் சுவார்சைல்ட், ஐன்ஸ்டீனின் சார்புக் கோட்பாடுகளின் சமன்பாடுகளை தீர்க்கும்போது, “கருப்பு விண்மீன்” போன்றதொன்றின் பண்புகளைக்கொண்ட ஒரு பொருள் இருக்கவேண்டு மென பொதுச்சார்புக் கோட்பாடு வெளிப்படுத்தியதை கண்டறிந்தார். ஆனால் 1930கள் வரை விஞ்ஞானிகள் கருந்துளைகள் பற்றி பெரிய ஈடுபாடு காட்டவில்லை.

1930களின் பின்னர், ஓபன்ஹைமர், சினைடர் மற்றும் வோல்கொப் போன்ற இயற்பியலாளர்கள் கருந்துளைகளின் ஆக்கம் பற்றியும், மற்றும் அவை பிரபஞ்சத்தில் இருப்பதற்கான சாத்தியக்கூறுகள் பற்றியும் தீவிரமாக ஆய்வு நடத்தினர். இவர்களின் ஆய்வுப்படி போதுமான அளவு திணிவு கொண்ட விண்மீன் ஒன்று தனது வாழ்நாளை முடித்துக்கொள்ளும் தருவாய் வரும்போது (எரிபொருள் தீர்ந்து!) தனது சொந்த ஈர்ப்பு விசையை எதிர்கொள்ள முடியாமல் சுருங்கி, கருந்துளையாகும். சாதாரணமாக ஒன்று தனது சொந்த ஈர்ப்பு விசையால் சுருங்கிவிடாமல் தடுப்பது, அதனுள் நடக்கும் அணுக்கரு இணைவு (fusion) மூலம் உருவாகும் அழுத்தமாகும். அணுக்கரு இணைவுச்செயற்பாடு நின்றுபோகும் தருவாயில், விண்மீனின் திணிவினால் ஏற்படும் ஈர்புவிசையை அந்த விண்மீனால் தடுக்க முடிவதில்லை, ஆதலால் சுருங்கி கருந்துளையாகிவிடும்.

எல்லா விண்மீன்களும் இவ்வாறு கருந்துளையாகுமா என்றால், இல்லை. உதாரணமாக நமது சூரியன் இன்னும் 5 பில்லியன் வருடங்கள் வரை வாழும், அத்தோடு அதன் எரிபொருள் முடிய, அது கருந்துளையாகது. காரணம், சூரியனது திணிவு, கருந்துளையாக மாற தேவைப்படும் ஈர்ப்புசக்தியை வழங்க போதுமானதல்ல. இவ்வாறு கருந்துளையாவதட்கு குறைந்தது சூரியனைப்போல மூன்றுமடங்கு திணிவுள்ள விண்மீன் வேண்டும்!

1940களின் பின்னர், கருந்துளைககள் பற்றிய ஆய்வு தீவிரமடைந்தது, பல்வேறுபட்ட இயற்பியலாளர்கள், ஐன்ஸ்டினின் பொதுச்சார்புக் கொள்கையின் விதிகளைப் பயன்படுத்தி கருந்துளைகளுக்கு பல்வேறு விதமான தீர்வுகளை கண்டறிந்தனர். 1963 இல் ராய் கேர் என்ற கணிதவியலாளர் பொ.சா.கோ வை பயன்படுத்தி சுற்றும் கருந்துளைகளுக்கான சமன்பாட்டை தீர்த்தார். 1965 இல் எஸ்ரா நியூமண், சுழலும் அதேவேளை மின்னேற்றமுள்ள கருந்துளைக்கான சமன்பாட்டை பூர்த்தி செய்தார்.

இப்படி பல்வேறு வகையான கருந்துளைகளை கோட்பாட்டு ரீதியாக பல்வேறு பட்ட இயற்பியலாளர்கள் முன்வைத்தாலும், நேரடியாக கருந்துளை ஒன்றை அவதானிப்பது தற்போதுவரை முடியாத காரியம். அனால் மறைமுகமாக, அவதானிக்க முடியும்.

நேரடியாக அவதானிக்க முடியாமல் இருப்பதால் என்னவோ, சில இயற்பியலாளர்கள் கருந்துளைகள் இயற்கையாகவே இல்லை என வாதிடுகின்றனர்.

1967இல் முதன் முதலாக ஜான் வீலர் என்ற இயற்பியலாளர் கருந்துளை என்ற பதத்தினை பயன்படுத்தினர். அதாவது பெரிய விண்மீன் ஒன்று தனது வாழ்நாளை முடித்துக்கொண்டு சூப்பர்நோவா என்ற பெருவெடிப்பின் மூலம் இறக்கும் பொது, மிக அடர்த்தியான சிறிய மையப்பகுதியை விட்டுச் செல்லும். இந்த சிறிய மையக்கோளத்தின் அடர்த்தியானது நமது சூரியனது அடர்த்தியை விட மூன்று மடங்குக்கு அதிகமாக இருப்பின், அது கருந்துளையாக மாறிவிடும் என்று ஐன்ஸ்டீனின் பொ.சா.கோ நமக்கு சொல்கிறது.

இந்த சிறிய மையக்கோளத்தின் அடர்த்தி மிக அதிகமாக இருப்பதனால் மற்றைய சக்திகளை விட, ஈர்ப்பு சக்தியின் ஆற்றல் அதிகரித்துவிடும். இந்த அதிகூடிய ஈர்ப்புவிசையால் அதனிலிருந்து எந்தவொரு மின்காந்த அலைகளும், வேறு விதமான துணிக்கைகளும் வெளிவரமுடியாமல் போவதால் இதை கருந்துளை எனலாம் என ஜான் வீலர் கருதினார்.

மிஸ்டர் கருந்துளையை நேரடியாக அவதானிக்க முடியாதது ஏன் என்பது பற்றி பாப்போம். கருந்துளைகள் எந்தவொரு மின்காந்த அலைகளையும் வெளிவிடுவதில்லை, ஆகவே நமது ஒளியியல் தொலைகாட்டிகளோ, அல்லது எக்ஸ்ரே, அகச்சிவப்புத் தொலைகாட்டிகளோ கருந்துளை விடயத்தில் நேரடியாக பயனற்றவை. ஆனால் கருந்துளையின் மிகப்பெரிய பலமே அதனது ஈர்புவிசையாயாகும், அதுவே அதனை காட்டிக்கொடுக்கக்கூடிய சமாச்சாரமும் ஆகும். நாம் நேரடியாக கருந்துளைகளை காணாவிடினும், அது, தன்னைச்சுற்றியுள்ள பிரபஞ்சப்பொருட்களின் மீது செலுத்தும் ஈர்ப்புவிசையால் கருந்துளைகளை நாம் கண்டுகொள்ளலாம்.

கருந்துளை ஒன்று மீனிடைத்தூசு அல்லது மீனிடைமுகில்கள் (interstellar dust / gas clouds) அருகில் வரும்போது, கருந்துளையானது, அத்தூசுகளை தன்பால் ஈர்த்து, தன்னைச் சுற்றி ஒரு திரள் வளர்ச்சியை (accretion) உருவாகிக்கொள்ளும். இதே போல ஒரு விண்மீனும், கருந்துளையின் பாதையில் குறுக்கிட்டால், கொக்கோகோலாவை ஸ்ட்ரோ போட்டு உறுஞ்சுவதைபோல விண்மீனையும் உருஞ்சிவிடும் இந்தக் கருந்துளை. இவ்வாறு உறுஞ்சப்பட்ட விண்மீனோ, மீனிடைத்தூசுகளோ சேர்ந்து உருவாகிய திரள் வளர்ச்சியானது, வேகமாக இந்த கருந்துளையை சுற்றும்போது, அவை வெப்பமடைந்து எக்ஸ் கதிர்கள் (x-ray) வெளிவருகின்றது. இவ் எக்ஸ் கதிர்களை எம்மால் அவதானிக்க முடியும்.

கருந்துளையை சுற்றியுள்ள திரள் வளர்ச்சியும், ஒரு நட்சத்திரத்தை கருந்துளை உறுஞ்சும் விதமும்

ஆக ஒரு விண்மீனின் இறப்பில் இருந்து கருந்துளை ஒன்று பிறக்கின்றது. எல்லா கருந்துளைகளும் விண்மீன்களின் வாழ்வின் முடிவில் நிகழும் சூப்பர்நோவா எனும் மீயொளிர் விண்மீன் வெடிப்பினால் உருவாவதில்லை, ஆனால் பெரும்பாலான கருந்துளைகள் இவ்வாறே உருவாகுகின்றன.

கருந்துளைகளிலும் பல்வேறு வித்தியாசமான கருந்துளைகள் உண்டு. அதேபோல ஒரு தமிழ் இயற்பியலாளரின் பங்களிப்பும் மிக முக்கியம், அவர்தான் சுப்பிரமணியன் சந்திரசேகர்.

முதலில் விண்மீன்களைப் பற்றிப் பாப்போம், கருந்துளைகளில் பெரும்பாலானவை விண்மீன்களின் வாழ்வின் முடிவில்தான் பிறக்கிறது என்று முன்னர் பார்த்தோம். ஆகவே விண்மீன்களின் வாழ்கையைப்பற்றி கொஞ்சம் அலசுவோம்.

நமது பிரபஞ்சத்தில் மிகல அதிகமாக காணப்படும் ஒரு மூலகம், ஹைட்ரோஜன் அல்லது ஐதரசன் மற்றும் ஹீலியம். நாம் இரவு வானில் பார்க்கும் ஒவ்வொரு புள்ளியும் விண்மீன்களே! நமது சூரியனைப் போல அளவுள்ளவை, சில சூரியனை விட சிறியவை, பல சூரியனை விட பல்லாயிரக்கணக்கான மடங்கு பெரியவை.

விண்மீன்கள் எப்படி உருவாகிறது என்று பார்க்கலாம்.

இந்தப் பாரிய பறந்து விரிந்த பிரபஞ்சத்தில் எண்ணிலடங்கா விண்மீன் பேரடைகள் அல்லது விண்மீன் திரள்கள் உண்டு. நமது சூரியன் இருக்கும் விண்மீன் பேரடை, பால்வீதி என்று அழைக்கப்படுகிறது. இவ்வாறான விண்மீன் பேரடைகளில் அதிகளவான வின்மீனிடை முகில்கள் (interstellar clouds) காணப்படுகின்றன. இவை பெரும்பாலும் ஐதரசனாலும் (கிட்டத்தட்ட 70%) மற்றும் ஹீலியத்தினாலும் (கிட்டத்தட்ட 20%) ஆக்கப்பட்டவை. அவற்றுள் மிகச்சொற்ப அளவு ஏனைய மூலகங்களும் காணப்படலாம். அவற்றில் அடர்த்தியாக உள்ளை வின்மீனிடை முகில்கள், பூமியில் இருந்து தொலைக்காட்டியால் பார்க்கும் பொது மிக அழகான தோற்றங்களில் தென்படும் இவற்றைத்தான் நெபுலா என வானியலாளர்கள் அழைக்கின்றனர்.

இந்த நெபுலாக்கள் தான் விண்மீன்களின் பெற்றோர்கள். நேபுலாகளில் ஏற்படும் அடர்த்தி வித்தியாசத்தால் ஒரு குறிப்பிட்ட இடத்தில் வாயுக்களின் அடர்த்தி அதிகரிக்க, அங்கு ஈர்ப்புவிசையும் தோன்றும். இந்த ஈர்ப்பு விசை காரணமாக மேலும் வாயுக்கள் அங்கு குவிய, ஒரு பந்தைப்போன்றதொரு திரள்ச்சியாக அது உருவெடுக்கும்.

இவ்வாறான திரள்ச்சியின் போது, வாயு மூலக்கூறுகள் (ஐதரசன்) மூலக்கூறுகள் ஒன்றுக்கொன்று மிக அருகில் வருவதால், அவற்றின் வெப்பநிலை அதிகரிக்கிறது, இவ் வெப்பநிலை தொடர்ச்சியாக அதிகரித்து, ஒரு கட்டத்தில் 10 மில்லியன் பாகை செல்சியஸ் அளவைக் கடக்கும் போது, ஒரு விண்மீனின் உயிர் மூச்சு தொடங்குகிறது. அதாவது அணுக்கரு இணைவு (fusion) எனப்படும் ஒரு செயல்பாடு தொடங்குகிறது. இது அந்த வாயுத்திரட்சியில் உள்ள ஐதரசனை, ஹீலியமாக மாற்றுகிறது, இவ்வாறு மாற்றமடையும் போது ஏற்படும் திணிவு வேறுபாடே, விண்மீனின் ஒளி, வெப்பம் மற்றும் இன்னும் பிற சக்திகளாக வெளிவிடப்படுகிறது. இந்த நிலையை அடைந்த விண்மீன்கள், முதன்மைத் தொடர் விண்மீன்கள் (main sequence star) என அழைக்கப்படுகிறது.

நெபுலா

ஒரு விண்மீன், நெபுலா போன்ற வாயுத் திரட்சியில் இருந்து முதன்மைத் தொடர் விண்மீனாக மாற கிட்டத்தட்ட 50 மில்லியன் வருடங்கள் எடுக்கிறது. ஒரு குறிப்பிட்ட நேபுலாவில் இருந்து பல விண்மீன்கள் (சிலவேளைகளில் நூற்றுக்கனக்கான) தோன்றும். நமது சூரியத்தொகுதிக்கு மிக அருகில் உள்ள உள்ளது ஒராயன் நெபுலா, இது 1300 ஒளியாண்டுகள் தூரத்தில் உள்ளது. இங்கு பல புதிய விண்மீன்கள் தற்போது உருவாவதை வானியலாளர்கள் அவதானிக்கின்றனர்.

ஒராயன் நெபுலா

இவ்வாறு முழுமையாக உருவாகிவிட்ட விண்மீன், முதன்மைத்தொடர் விண்மீன் எனப்படும். நமது சூரியன் ஒரு முதன்மைத்தொடர் விண்மீன் ஆகும், அதே போல இந்த முதன்மைத்தொடர் பருவத்தில் கிட்டத்தட்ட 10 பில்லியன் வருடங்கள் வரை வாழும்!

விண்மீன்களின் மையப் பகுதியில் நடக்கும் இந்த அணுகரு இணைவே, இந்த விண்மீன்கள், அவற்றின் ஈர்ப்பு விசையால் மேற்கொண்டு சுருங்கிவிடாமல் இருக்க தேவையான வெளிநோக்கிய அழுததை வழங்குகிறது.

விண்மீன்களின் அளவிற்கும், திணிவிற்கும் ஏற்ப அதன் வாழ்க்கைக்காலமும், அதன் முடிவும் தங்கியுள்ளது, அவற்றைப் பற்றி அடுத்ததாக பார்க்கலாம்.

விண்மீன்களின் வாழ்க்கை என்பது அதன் இறப்போடு முடிவதில்லை. விண்மீன்கள், தனது எரிபொருளை, அதாவது ஐதரசனை முடிக்கும் வரை முதன்மைத் தொடர் பருவத்திலேயே இருக்கும். பொதுவாக விண்மீனில் இருக்கும் ஐதரசன் அனைத்தும் ஹீலியமாக மாறியவுடன் விண்மீனின் அணுக்கருச் செயற்பாடு முடிவுக்கு வருகிறது, இந்நிலையில் விண்மீனின் அளவை தக்கவைத்திருக்கும் வெளிநோக்கிய அழுத்த சக்தியும் இல்லாமல் போகவே, விண்மீனின் திணிவினால் உருவாகிய ஈர்ப்புசக்தியை வெல்லமுடியாமல் விண்மீனின் மையப்பகுதி சுருங்கத் தொடங்கும். இவ்வாறு சுருங்குவதால் மையப்பகுதியின் வெப்பநிலை மேலும் அதிகரித்து விண்மீனின் மேற்பகுதி வெளிநோக்கி விரிவடையும். இப்படி விரிவடைவதால் இந்த வெளிப்பகுதியின் வெப்பநிலை குறைவடையும். இவ்வாறு விரிவடையும் விண்மீன் சிவப்பரக்கன் (red giant) எனப்படும்.

இன்னும் கிட்டத்தட்ட ஐந்து பில்லியன் வருடங்களில், நமது சூரியனும் ஒரு சிவப்பரக்கன் ஆக மாறிவிடும். இந்த சிவப்பரக்கனின் மேற்பகுதிக்குள் நமது பூமியின் சுற்றுப்பாதையும் அடங்கிவிடும், அதாவது நமது சூரியன் சிவப்பரக்கனாக மாறும் போது அது நமது பூமியையே விழுங்கும் அளவிற்கு பெருத்துவிடும்.

சில விண்மீன்கள் போதுமானளவு திணிவுடயதாக இருப்பின், இவ்வாறு ஐதரசன் அனுப்பிணைவுச் செயல்பாடு முடிந்தவுடன் சுருங்கும் மையப்பகுதி போதுமானளவு பெரிதாக இருப்பதனால், ஐதரசனில் இருந்து வந்த ஹீலியமும் அணுப்பிணைவுச் செயல்பாட்டுக்கு உட்பட்டு மேலும் திணிவு அதிகமான மூலகங்களை தோற்றுவிக்கிறது, இந்தச் செயல்பாடு இரும்பு உருவாகும் வரை நடைபெறுகிறது.

ஐதரசனில் இருந்து இரும்பு வரை, படிப்படியாக நிகழும் அணுப்பிணைவுச் செயல்பாட்டின் மூலம் மேலதிக் சக்தி உருவாகும், இதுவே விண்மீன்களின் மூலசக்தி, அனால் இரும்பை அணுப்பிணைவுக்கு உட்படுத்தும் போது மேலதிக சக்தி உருவாகாது, மாறக இரும்பை அனுப்பிணைவுக்கு உட்படுத்தவே மேலதிக சக்தி வேண்டும், இதனால்த்தான் ஐதரசனில் இருந்து ஹீலியம், அதிலிருந்து லிதியம் என்று தொடக்கி நடக்கும் அணுப்பிணைவுச் செயல்பாடு இறுதியாக இரும்பை அடைந்தவுடன் முடிவுக்கு வருகிறது.

ஹீலியத்தில் இருந்து படிப்படியாக இரும்பு உருவாகும் வரையான அணுப்பிணைவு சொற்ப காலத்திலேயே நடந்து முடிவதால், விண்மீனின் மையப்பகுதியின் ஸ்திரத்தன்மை குலையும். இது அந்த விண்மீனின் புறப்பபகுதிகளை வெளிநோக்கி பீச்சி எரியும், சில வேளைகளில் பிரகாசமாக எரியும், மற்றும் சிலவேளைகளில் அப்படியே மெதுவாக இறந்துவிடும்.

இவ்வாறு ஒரு விண்மீன் பல்வேறு பட்ட விதங்களில் இறப்பதற்கு காரணம் அதன் திணிவு ஆகும், ஒரு விண்மீனின் திணிவைப் பொறுத்து அதன் இறுதிக்காலமும் தீர்மானிக்கப்படும்.

இனி விண்மீனின் திணிவைப்பொறுத்து, அதன் இறுதிக்காலத்தின் பின் எவ்வாறு மாறுகிறது என்று பார்க்கலாம்.

சராசரி திணிவுகொண்ட விண்மீன்கள், அதாவது நமது சூரியனது அளவு, அல்லது சூரியனைப்போல 1.4 மடங்கு வரை திணிவுகொண்ட விண்மீன்கள், இறுதியாக வெள்ளைக்குள்ளன் என்ற நிலையை அடைகிறது.

விண்மீனின் புறப்பகுதிகள் அனைத்தும் வெளிநோக்கி வீசப்பட்டு, இறுதியாக விண்மீனின் மையப்பகுதி மாத்திரம் எஞ்சி இருக்கும். இந்த மையப்பகுதி அண்ணளவாக நமது பூமியின் அளவில் இருக்கும்.

கழுதை தேய்ந்து கட்டெறும்பு ஆவது போல (?!), பெரிய சூரியனைப் போன்ற விண்மீன் சுருங்கி பூமியின் அளவை அடையும். இதுவே வெள்ளைக்குள்ளன். இது மேலும் தனது சொந்த ஈர்ப்புசக்தியால் சுருங்குவதில்லை. அதற்கு காரணம் இலத்திரன் அழுத்தம் ஆகும்.

ஓர் வெள்ளைக்குள்ளனாக மாறிய நட்சத்திரத்தில் என்ன நிகழ்கிறது என்று நமக்கு குவாண்டம் இயற்பியல் விளக்குகிறது. அணுவை வேகமாக சுற்றும் இலத்திரன்கள் ஒருவிதமான அழுத்தத்தை உருவாக்குகின்றன, இந்த அழுத்தம், வெள்ளைக்குள்ளன் மேலும் சுருங்குவதை தடுக்கிறது.

அதேபோல மையப்பகுதியின் திணிவு அதிகமாக இருப்பின், அதன் அடர்த்தியும் அதிகமாக இருக்கும், ஆகவே, திணிவு அதிகமான வெள்ளைக்குள்ளன் அளவில் சிறியதாகவும், திணிவு குறைவான வெள்ளைக்குள்ளன் ஒப்பீட்டு அளவில் பெரியதாகவும் இருக்கும்.

ஆனால் ஒரு விண்மீனின் மையப்பகுதியின் திணிவு, சூரியனின் திணிவைப்போல 1.4 மடங்கைவிட அதிகமாக இருப்பின், அல்லது மொத்த விண்மீனின் திணிவு சூரிய திணிவைப்போல எட்டு மடங்குக்கு மேல் இருப்பின், அதன் விதி இன்னும் உக்கிரமாக இருக்கும்! மீயோளிர் நட்சத்திர வெடிப்பு / சூப்பர்நோவா எனப்படும் மிகப்பிரமாண்டமான வெடிப்புடன் குறிப்பிட்ட விண்மீன் தனது நிலையை இழக்கிறது.

SN 1987a – சூப்பர்நோவா எச்சம் – 160000 ஒளியாண்டுகள் தூரத்தில் இருக்கும் பெரிய மகிலன் முகில் விண்மீன்பேரடையில் இருக்கிறது

முன்னர் கூறியது போல, ஒரு விண்மீன், ஐதரசனில் இருந்து படிப்படியாக அணுக்கரு இணைவு மூலம் அதன் மையப்பகுதி இரும்பாக மாறியவுடன், மேற்கொண்டு அணுகரு இணைவு மூலம் சக்தியை உருவாக்க முடியாத விண்மீன், தனது அளவை பேணத்தேவையான அழுத்தத்தை இழக்கிறது. மையப்பகுதியின் திணிவு 1.4 சூரியத் திணிவைவிட அதிகமாக இருக்கும் போது, அதன் ஈர்ப்பு விசையை தாங்காமல், கிட்டத்தட்ட 10000 கிலோமீட்டர் விட்டமான விண்மீனின் மையப்பகுதி, 50 கிலோமீட்டருக்கும் சிறிதாக சுருங்குகிறது. அவ்வேளையில் அதன் வெப்பநிலை 100 பில்லியன் பாகை செல்சியஸ்வரை அதிகரிக்கிறது. இவ்வாறு சுருங்கும் போது, விண்மீனின் மேற்பகுதியும் சுருங்கினாலும்,  அதிகூடிய வெப்பநிலையால், திடீரென பெரிதாக விரிந்து, அளவுக்கதிகமான சக்தியை வெளியிட்டு வெடிக்கிறது.

சில சூப்பர்நோவாக்கள் ஒரு சில வாரங்கள் வரை இவ்வாறு அளவுக்கதிகமான சக்தியை வெளியிடும். இவ்வாறு வெளியிடும் சக்தி மிக மிக அதிகம் என்பதால் அந்த சூப்பர்நோவா தானிருக்கும் விண்மீன் பேரடையை (galaxy) விட மிகப்பிரகாசமாக ஒளிரும்.

இவ்வாறு சூப்பர்நோவாவாக முடிந்த விண்மீனில் இன்னும் ஒரு பகுதி எஞ்சி இருக்கும், அதுதான் மிகச் சிறிதாக சுருங்கிய அந்த விண்மீனின் மையப்பகுதி. விண்மீனின் திணிவிற்கு ஏற்ப அந்த மையப்பகுதியானது ஒன்றில் நியூட்ரான் விண்மீனாகவோ அல்லது கருந்துளையாகவோ மாறும்.

இயற்கையின் விநோதங்களில் கருந்துளையைப் போலவே, இன்னொரு முடிவில் தொக்கி நிற்பது இந்த நியூட்ரான் விண்மீன்கள். சூரியனை விட பெரிய விண்மீன்கள், கிட்டத்தட்ட அந்த விண்மீன்களின் மையப்பகுதி, நமது சூரியனைப்போல 1.4 தொடக்கம் 3 மடங்கு திணிவுள்ளதாய் அமையும்போது, அதனது எரிபொருளை முடித்துக்கொண்டு மீயோளிர் விண்மீன் பெருவெடிப்பாக (சூப்பர்நோவா) சிதற, அதன் மையப்பகுதியில் எஞ்சி இருப்பது இந்த நியூட்ரான் விண்மீனாகும்.

நியூட்ரான் விண்மீன்களின் அளவு மிக மிக சிறிது. ஏன் இவ்வளவு சிறிதாக இருக்கிறது என்று பார்ப்பதற்கு, முதலில் ஏன் இந்த பெயர், நியூட்ரான் விண்மீன்? ஆராய்வோம்.

நாம் பார்க்கும், உணரும் என எல்லா பொருட்களும் அணுக்களால் தான் ஆக்கப்பட்டுள்ளது. அணுக்களை நாம் அடிப்படை ஆக்கக்கூறு என்று கருதலாம், ஆனாலும் அணுக்கள் என்பது தனிப்பட்ட வஸ்து அல்ல. அணுக்கள் கூட, நியூட்ரான், ப்ரோடான், ஏலேக்ட்ரோன் போன்ற துணிக்கைகள் ஒன்று சேர்ந்து உருவாக்கப்பட்டவை. மேலும் ஒரு தகவல், இந்த நியூட்ரான், ப்ரோடான் துணிக்கைகளும், குவார்க் எனப்படும் இன்னும் சிறிய துணிக்கைகளால் ஒன்றுசேர்ந்து ஆக்கப்பட்டவை. (இன்னுமொரு உபரித்தகவல்: இந்த குவார்க் துணிக்கைகள் கூட ஸ்ட்ரிங் எனப்படும், குவர்க்கை விட பல கோடிக்கணக்கான மடங்கு சிறிய ஸ்ட்ரிங் எனப்படும் அமைப்பினால் உருவாக்கப்பட்டது என்று இயற்பியலில் ஒருவகையான, ஸ்ட்ரிங் இயற்பியல் கோட்பாடு சொல்கிறது!)

விடயத்திற்கு வருவோம், ஆக எம்மை, இந்த சூரியனை, இந்த சூரியனை போல எல்லா விண்மீன்களையும் ஆக்கியுள்ள கட்டமைப்பு அணுக்களால் ஆனது. அணுவின் கட்டமைப்பை பற்றி இங்கு பார்க்கவேண்டும். ஒரு அணுவின் மையப்பகுதியில் அணுக்கரு காணப்படும், அது ப்ரோடான், நியூட்ரான் ஆகியவற்றால் ஆக்கப்பட்டிருக்கும். இந்த அணுக்கருவை சுற்றி இலத்திரன்கள் ஒரு முகில் போல சுழன்றுகொண்டிருக்கும். இந்தப் பாடப்புத்தகங்களில் காட்டுவது போன்று அணுக்கருவை சுற்றிவரும் இலத்திரன்களை, சூரியனை சுற்றி வரும் கோள்களைப்போல காட்டமுடியாது (ஏன்?).

இங்கு கவனிக்க வேண்டிய விடயம், ஒரு அணுவின் திணிவில் 99.9 வீதமான திணிவு, அணுக்கருவில் தான் இருக்கும், ஆனால், அனுகருவை சுற்றிவரும் இலத்திரன் முகிலின் அளவோடு ஒப்பிடும் போது ஒரு லட்சத்தில் ஒரு பங்கு மட்டுமே அணுக்கருவின் அளவு இருக்கும். ஒரு ஒப்பீட்டை சொல்கிறேன். ஒரு அணுவை, கிரிக்கெட் மைதானத்தின் அளவு பெரிதாகினால், அணுக்கருவின் அளவு வெறும் கிரிக்கெட் பந்தின் அளவில் மாத்திரமே இருக்கும், இந்தப்பந்தை, அணுகரு என்று கொண்டு, அதை மைதானத்தின் நடுப்பகுதியல் வைத்தால், இந்த் இலத்திரன்கள், அந்த மைதானத்தின் வெளி எல்லையில் சுற்றிவரும். இப்போது உங்களுக்கு அணுவின் கட்டமைப்பில் எவ்வளவு இடைவெளி இருக்கிறது என்று புரிந்திருக்கும். ஆக, அணுவில் கிட்டத்தட்ட 99.99% வெற்றுவெளியே இருக்கிறது!

ஒரு கால்பந்து மைதானத்தின் அளவுள்ள கல்லொன்றில் இருக்கும் அணைத்து அணுக்களில் இருந்தும் இந்த இடைவெளியை நீங்கிவிட்டால், அந்தக்கல்லானது கிட்டத்தட்ட ஒரு மண் துணிக்கையின் அளவிற்கு வந்துவிடும், ஆனால் அதன் திணிவு நான்கு மில்லியன் டன்! இதே விளையாட்டுதான் இந்த நியூட்ரான் விண்மீன்களிலும் நிகழ்கிறது.

சூப்பர்நோவாவின் பின் மையப்பகுதியில் எஞ்சி இருக்கும் நியூட்ரான் நட்சத்திரம்.

போதுமானளவு பெரிய விண்மீன்கள் சூப்பர்நோவாவாக வெடிக்கும் போது, மிஞ்சும் மய்யப்பகுதின் ஈர்ப்புவிசையால், அங்கிருக்கும் அணுக்கள் ஒன்றுக்கொன்று மிக அருகில் வர, அணுக்களில் உள்ள இடைவெளி குறைகிறது, அதேபோல எதிர் ஏற்றம் கொண்ட இலத்திரன்கள், நேர் ஏற்றம் கொண்ட ப்ரோட்டன்களுடன் இணைந்து நியூட்ரான்களாக மாறி, கடைசியாக அங்கு வெறும் நியூட்ரான்கள் மட்டுமே எஞ்சி இருக்கும். இந்த நியூட்ரான்கள் இடைவெளி இன்றி ஒன்றுக்கொன்று மிக அருகில் இருப்பதால், இந்த நியூட்ரான் நட்சத்திரங்கள் அளவில் மிகச்சிறிதாக இருக்கும், கிட்டத்தட்ட 10km இலிருந்து 30km வரையான விட்டத்தைகொண்டிருக்கும். ஆனாலும் இவற்றின் திணிவு மிக மிக அதிகம், மேற்சொன்ன விளையாட்டு மைதான அளவுள்ள கல்லின் உதாரணத்தை கொண்டு ஒப்பிட்டு பாருங்கள்.

இந்த நியூட்ரான் விண்மீன்களுக்கு ஒரு விசித்திரப் பண்பு உண்டு, அதுதான் அதற்கு இருக்கும் மிக மிக வலிமையான காந்தப்புலம் அதாவது பூமிக்கு இருப்பதை போல, ஆனாலும் பூமியின் காந்தபுலத்தை காட்டிலும், நூறு ட்ரில்லியன் மடங்கு அதிகமான கந்தப்புலத்தை இந்த, பூமியன் அளவில் ஆயிரத்தில் ஒரு பங்கே உள்ள நியூட்ரான் நட்சத்திரங்கள் கொண்டுள்ளன.

இந்த அளவுக்கதிகமான காந்த சக்தி, நியூட்ரான் விண்மீன்களுக்கு மிகப்பெரிய சக்தியை வழங்குகிறது. அவற்றைப்பற்றி அடுத்ததாக பார்க்கலாம்.

நியூட்ரான் விண்மீன்கள் மிகுந்த காந்தப்புலத்தை கொண்டவை, சொல்லப்போனால் இந்த பிரபஞ்சத்தில் அதிகூடிய காந்தப்புலத்தை கொண்ட அமைப்பாக இந்த நியூட்ரான் விண்மீன்களே காணப்படுகின்றன. அதிலும் மக்னட்டார் (Magnetar) எனப்படும் நியூட்ரான் விண்மீன்கள் பூமியின் காந்தப்புலத்தைப்போல குவார்ட்ட்ரில்லியன் மடங்கு (குவார்ட்ட்ரில்லியன் என்பது, 1 இற்குப் பின்னால் 15 பூஜியங்கள் வரும் இலக்கம்!) அதிகமான காந்தபுலத்தை கொண்டுள்ளன.

ஏன் இந்த நியூட்ரான் விண்மீன்கள் இப்படி அதிகூடிய காந்தப்புலத்தை கொண்டுள்ளன என்று பார்க்கலாம்.

சாதாரணமாக விண்மீன்களுக்கு குறைந்தளவு காந்தப்புலம் இருக்கும், இவ்வாறு காந்தபுலம் இருக்கும் விண்மீன் ஒன்று சூப்பர்நோவாவாக அழியும் போது, இந்த விண்மீனின் மையப்பகுதி சுருங்குவதால், அதற்கு இருக்கும் காந்தப்புலமும் சேர்ந்தே சுருங்குகிறது. இவாறு சுருங்கும் போது, இந்த காந்தபுலத்தின் வீரியம், சுருங்கிய வீதத்தின் அடிப்படையில் அதிகரிக்கும்.

நண்டு நேபுலா – அதன் மையத்தில் ஒரு துடிப்பலை

சரி, ஒரு உதாரணம் மூலம் விளக்குகிறேன், நமது சூரியனுக்கு இருக்கும் காந்தப்புலத்தின் அளவைக்கொண்ட (சூரியனது சராசரி மேற்பரப்பு காந்தபுலம் கிட்டத்தட்ட 5 Gauss, பூமியின் மேற்பரப்பில் காந்தபுலம், கிட்டத்தட்ட 1 Gauss, என்னடா, சூரியனது காந்தபுலம் அவ்வளவுதானா என எண்ணவேண்டாம், சூரியன் பூமியை விட பலமடங்கு பெரியது, ஆகவே அதன் மொத்த காந்தபுலத்தின் சக்தி பூமியை விட பலமடங்கு அதிகம்) ஒரு விண்மீன், நியூட்ரான் நட்சத்திரமாக சுருங்கும் போது, அதன் காந்தபுலத்தின் வீரியம் கிட்டத்தட்ட சுருங்கிய விகிதமான 1.25×1014 மடங்காக அதிகரிக்கும். அதாவது 1 Gauss ஆரம்ப காந்தப்புலம், 56 மில்லியன் Gauss களாக அதிகரிக்கும்.

ஆனால் சூரியனது அளவுகொண்ட ஒரு விண்மீன் சூப்பர்நோவாவாக வெடிக்காதே, சாதரணமாக அவ்வாறு வெடிக்கக்கூடிய விண்மீன் 100 Gauss வரை மேற்பரப்பு காந்தபுலத்தை கொண்டிருக்கும், அவ்வாறு 100 Gauss அளவு காந்தபுலத்தை கொண்டுள்ள விண்மீன் வெடித்து நியூட்ரான் விண்மீன் உருவாகும் போது அதன் காந்தப்புலம் கிட்டத்தட்ட 1 ட்ரில்லியன் Gauss வரை அதிகரிக்கும்! கீழ் வரும் அட்டவணையில் பிரபஞ்சத்தில் உள்ள பல்வேறுபட்ட அமைப்புகளுக்கு இருக்ககூடிய அண்ணளவான காந்தபுலத்தின் அளவை குறிபிட்டுள்ளேன்.

பிரபஞ்சக்காந்தபுலத்தின் அளவு	0.00001 Gauss
சூரியப்புயல்	0.00005 Gauss
வின்மீனிடை முகில்கள்	0.001 Gauss
பூமியின் மேற்பரப்பு	1 Gauss
சூரியனது மேற்பரப்பு	5 Gauss
பாரிய நட்சத்திரம்	100 Gauss
குளிர்சாதனப்பெட்டியின் கதவில் ஓட்டும் காந்தம்	100 Gauss
சூரியப்புள்ளியின் புலம்	1000 Gauss
வியாழனின் காந்தபுலம்	1000 Gauss
காந்தபுலம் அதிகம் கொண்ட நட்சத்திரம் (BD+54 2846)	12,000 Gauss
வெள்ளைக்குள்ளன்	1,000,000 Gauss
நியூட்ரான் நட்சத்திரத்தின் மேற்பரப்பு	1,000,000,000,000 Gauss
மக்னட்டார்	1,000,000,000,000,000 Gauss

துடிப்பலைகள் / பல்சார்கள் (Pulsar)

நியூட்ரான் விண்மீன்களுக்கு இன்னுமொரு பண்பு உண்டு. இவை மிக வேகமாக சுழலக்கூடியவை. இவ்வாறு சுழலும் நியூட்ரான் விண்மீன்கள், பல்சார் / துடிப்பலை (Pulsar) என அழைக்கப்படுகிறது. ஏற்க்கனவே அதிக சக்திவாய்ந்த காந்தப்புலத்தைக் கொண்டுள்ள இந்த நியூட்ரான் விண்மீன்கள், மிக வேகமாக சுற்றும் போது, ஒரு சக்திவாய்ந்த டைனமோ போல செயல்பட்டு, மிக மிக அதிகமான மின்சக்தியை தோற்றுவிக்கிறது. சர்வசாதாரணமாக ஒரு பல்சார் குவார்ட்ட்ரில்லியன் வோல்ட் மின்னழுத்த வேறுபாட்டை உருவாக்கும். இவை கிட்டத்தட்ட பூமியில் தோன்றும் மின்னல்களில் உள்ள மின்னழுத்த வேறுபாட்டை விட 30 மில்லியன் மடங்கு அதிகம்!

துடிப்பலையின் துருவத்தில் இருந்து வெளிப்படும் கதிர்வீச்சு

இவ்வாறு தோன்றிய மிக அதிகமான மின்அழுத்த வேறுபாடு மற்றும் அதிகளவான காந்தபுலம், உயர் சக்திகொண்ட துகள்களை தோற்றுவிக்கிறது. இந்த துகள்கள், ரேடியோ அலைவீச்சில் இருந்து காமா அலைவீச்சு வரை மிக சக்திவாய்ந்த கதிர்வீச்சை தோற்றுவிக்கிறது. இந்த கதிர்வீச்சு இந்த துடிப்பலை விண்மீனின் துருவங்களினூடாக ஒரு கலங்கரைவிளக்கத்தில் உள்ள ஒளி போல . இருபக்கமும் பாயும், அதேவேளை இந்த துடிப்பலை விண்மீன் வேகமாக சுற்றிக்கொண்டு இருப்பதனால், இந்த இரண்டு துருவங்களிலும் இருந்து வரும் கதிர்வீச்சு பூமிக்கு விட்டு விட்டு வருவதால் இதற்கு துடிப்பலை என்று பெயர் வந்தது.

இங்கு மிக முக்கியமான விடயம், துடிப்பலைகளின் துருவங்கள் பூமியை நோக்கி இருந்தால் மட்டுமே, எம்மால் இந்த துடிப்பலை விண்மீன்களை பார்க்கமுடியும். அதாவது, நீங்கள் கடலில் கப்பலில் பயணிக்கும் போது, கலங்கரைவிளக்கம் இருக்கும் பக்கத்தை பார்த்தல் தான் அதன் ஒளி தெரிவதைப்போல.

இந்த துடிப்பலைகள் முதன் முதலில் 1967இல் தான் கண்டுபிடிக்கப்பட்டது. இன்றுவரை கிட்டத்தட்ட ஆயிரம் துடிப்பலை விண்மீன்களை நாம் கண்டறிந்துள்ளோம். அதிலும் குறிப்பாக நண்டு நெபுலாவில் உள்ள துடிப்பலை மிக சக்திவாய்ந்த ஒரு துடிப்பலை, அண்ணளவாக 6000 ஒளியாண்டுகள் தூரத்தில் உள்ள இந்த துடிப்பலை, ஒரு செக்கனுக்கு 30 தடைவைகள் துடிக்கிறது (அப்படியென்றால், ஒரு செக்கனுக்கு 15 தடவைகள் தனது அச்சில் சுழல்கிறது என்று பொருள்!)

இப்படி மிக வேகமாக சுழலும் துடிப்பலை விண்மீன்கள் காலத்திற்கும் தொடந்து சுற்றிக்கொண்டு இருப்பதில்லை. இந்த துடிப்பலையில் இருந்து வெளிவரும் கதிர்வீச்சு காரணமாக காலப்போக்கில் இந்த விண்மீன்களின் சுழற்ச்சி வேகம் குறைகிறது. துடிப்பலையின் சுழற்ச்சி வேகம் ஒரு கட்டத்தை விட குறையும் போது, துருவங்களில் இருந்துவரும் கதிர்வீச்சு நின்றுவிடும் (சைக்கில் டைனமோவை நினைத்துப்பாருங்கள், ஒரு அளவு வேகத்தைவிட குறைவாக நீங்கள் பயணிக்கும் பொது, டைனமோ மூலம் ஒளிரும் முன்விளக்கு அணைந்துவிடும்). அண்ணளவாக ஒரு துடிப்பலை விண்மீன் ஒன்று உருவாக்கி, 10 இல் இருந்து 100 மில்லியன் வருடங்களில் அதன் துடிப்பலை நின்றுவிடும்.

ஆக, வானியலாளர்கள், இந்தப் பிரபஞ்சத்தில் உருவாகிய துடிப்பலைகளில் 99% ஆனவை ஏற்கனவே அணைந்துவிட்டது (துடிப்பதை நிறுத்திவிட்டது) என கருதுகின்றனர், ஏனெனில் பிரபஞ்சம் தோன்றி 13.7 பில்லியன் வருடங்கள் ஆகிறதே!

நியூட்ரான் விண்மீன்களைப் பற்றி நிறைய விடயங்களை பார்த்துவிட்டோம், முடிப்பதற்கு முன் இறுதியாக ஒருவிடயம்.

நியூட்ரான் விண்மீன்கள் சிலவேளைகளில் இரட்டை விண்மீன் தொகுதியில் தோன்றலாம். இப்படி இரட்டை விண்மீன்களில் ஒன்று நியூட்ரான் விண்மீனாக மாறும் பட்சத்தில், மற்றைய விண்மீனில் இருக்கும் வஸ்துக்களை இந்த நியூட்ரான் விண்மீன் உறுஞ்சத் தொடங்கிவிடும். இவ்வாறு உறுஞ்சப்படும் வாயுக்கள், துணிக்கைகள், இந்த நியூட்ரான் விண்மீனைச் சுற்றி மிக வேகமாக சுழலும் ஒரு தகட்டைப்போல உருவெடுத்துவிடும். இவ்வாறு மிகவேகமாக சுழலும் தட்டு, அதிகளவான எக்ஸ் கதிர்வீச்சை உருவாகுகிறது.

அருகில் இருக்கும் நட்சத்திரத்தை உருஞ்சும் நியூட்ரான் நட்சத்திரம்

பிரபஞ்சத்தில் உள்ள எல்லா விண்மீன் வகைகளையும் விட, கருந்துளைக்கு மிக ஒத்த பண்புகளை கொண்டது இந்த நியூட்ரான் விண்மீன்கள்தான். ஆனால் அவைகூட கருந்துளையின் வில்லத்தனத்திற்கு ஏணி வைத்தும் எட்டிப்பார்க முடியாதளவு தள்ளியே இருக்கிறது.

நமது சூரியனை விட 1.4 தொடக்கம் 3 மடங்கு திணிவுள்ள மையப்பகுதியை கொண்ட விண்மீன்கள் நியூட்ரான் விண்மீன்களாக மாறும் என்று நாம் பார்த்தோம். அப்படியென்றால் ஒரு விண்மீனின் மையப்பகுதியின் திணிவு 3 சூரியத் திணிவைவிட அதிகமாக இருப்பின் என்ன நடக்கும்?

ஒரே வார்த்தையில் அது கருந்துளையாகிவிடும் என்று சொல்லவிடாமல், அது எவ்வாறு நடைபெறுகிறது என்று படிப் படியாக பார்போம்.

நான் முன்னரே சொன்னதுபோல, கருந்துளைக்கான ஐடியா, நியூட்டன் காலத்திலேயே இருந்திருந்தாலும், ஐன்ஸ்டீனின் பொதுச் சார்புக் கோட்பாடே முதன் முதலில் கருந்துளை இருப்பதற்கான கணித ரீதியான சமன்பாடுகளை வெளிக்கொண்டு வந்தது. 1915இல் ஐன்ஸ்டீன் தனது சார்புக் கோட்பாட்டை வெளியிட்டாலும், அவரது சார்புச் சமன்பாடுகளுக்கு தீர்வை முதன் முதலில் கண்டவர், கார்ல் சுவர்ட்சில்ட் (Karl Schwarzschild 1873 – 1916). கார்லிற்கு பின்னர் வேறு பலரும் இந்த தீர்வை உறுதிப்படுத்தினாலும், இன்று இந்த தீர்வு “சுவர்ட்சில்ட் ஆரை” (Schwarzschild radius) என அழைக்கப்படுகிறது.

சுவர்ட்சில்ட் ஆரை என்றால் என்னவென்று பார்த்துவிடுவோம். அதாவது, சுவர்ட்சில்ட் ஆரை என்பது ஒரு கோளத்தின் ஆரை – ஒரு பொருளின் திணிவை, இந்த சுவர்ட்சில்ட் ஆரை அளவுள்ள கோளத்தின் அளவுக்கு சுருக்கினால், இக் கோளத்தின் விடுபடு திசைவேகம் (escape velocity) ஒளியின் வேகமாக இருக்கும்! ஆக அந்தக் கோளத்தில் இருந்து ஒளியும் தப்பிக்க முடியாது. 1920 களில் சுவர்ட்சில்ட் இதை வெளியிட்ட போது, ஒருவரும் இதை கருந்துளைகளோடு ஒப்பிட்டு பார்க்கவில்லை. பெரும்பாலான கணிதவியலாலர்களும், இயற்பியலாளர்களும் இது பொதுச் சார்புக் கோட்பாட்டில் உள்ள ஒரு முரண்பாடு என்றே கருதினர். ஆனால் 1931இல் சுப்பிரமணியன் சந்திரசேகர் ஒரு புதிய பாதையை தொடக்கிவிட்டார்.

சுபிரமணியன் சந்திரசேகர்

சுப்பிரமணியன் சந்திரசேகர் (1910-1995) – கருந்துளைகள் சார்ந்த இயற்பியல் விதிகளுக்கான முன்னோடியான கணிதவியல் சமன்பாடுகளை நிறுவியதற்காக நோபல் பரிசு பெற்ற ஒரு தமிழர்! இந்தியாவில் பிறந்து வளர்ந்து, சிகாகோ பல்கலைகழகத்தில் பேராசிரியராக இருந்தவர். இவர் கருந்துளைகள் பற்றிய ஆராய்ச்சிக்கு என்ன செய்தார் என்று பார்ப்போம்.

வெள்ளைக் குள்ளன் (white dwarf) என்று ஒரு வகையான விண்மீன்களைப் பற்றி முன்பு சொல்லியிருந்தேன் (வெள்ளைக்குள்ளனைப் பற்றி பாகம் 5 இல் பார்த்துள்ளோம்). இந்த வெள்ளைக் குள்ளனின் அளவு சூரிய திணிவில் 1.44 மடங்குக்கு அதிகமாக இருக்க முடியாது என்று சந்திரசேகர், பொதுச் சார்புக் கோட்பாட்டு விதிகளைப் பயன்படுத்தி கணக்கிட்டார், அதுவும் தனது 19ஆவது வயதில்! (தற்போது நீங்கள் திறந்திருக்கும் வாயை மூடிக்கொள்ளலாம்). இன்று இந்த திணிவின் அளவு சந்திரசேகர் வரையறை என்று அழைகப்படுகிறது. புதிய ஆய்வின் படி, தற்போது ஏற்றுக்கொள்ளப்பட்ட இந்த திணிவின் அளவு 1.39 சூரியத் திணிவுகளாகும்.

நாம் ஏற்கனவே பார்த்தபடி (பாகம் 5இல்), ஒரு வெள்ளைக்குள்ளனாக மாறிய விண்மீன் தனது ஈர்ப்புவிசையால் மேலும் சுருங்காமல் அதன் நிலையை பேணுவதற்கு இலத்திரன்களின் அழுத்தம் காரணம். அப்படியென்றால், சந்திரசேகரின் கணக்குப்படி, ஒரு விண்மீனின் மைய்யப்பகுதியின் திணிவு 1.44 மடங்கு சூரியத் திணிவைவிட அதிகமாக இருப்பின், இலத்திரன்களின் அழுத்தம் கூட, அதன் ஈர்ப்பு விசைக்கு தாக்கு பிடிக்காது. ஆகவே அந்த விண்மீன் முடிவிலி அளவு சுருங்கிவிடும்! அல்லது எவ்வளவு தூரம் சுருங்கும் என பொ.சா.கோவை வைத்து கணக்கிட முடியாது என்று சந்திரசேகர் காட்டினார்.

ஆர்தர் எடிங்க்டன்

வில்லன் இல்லாவிட்டால் கதை சூடுபிடிக்காதல்லவா! வந்துவிட்டார் வில்லன் ஆர்தர் எடிங்க்டன் (Arthur Eddington). சந்திரசேகர் இவரிடம்தான் ஆராய்ச்சி உதவியாளராக இருந்தார். சந்திரசேகரின் இந்த கணிதவியல் முடிவை எடிங்க்டன் ஏற்றுக் கொள்ளவில்லை. அப்போதிருந்த பெரும்பாலான இயற்பியலாளர்கள் போல, கருந்துளை என்று ஒன்று இயற்கையில் இருக்கும் என எடிங்க்டன் நம்பவில்லை, அதுவொரு பொ.சா.கோவில் உள்ள கணிதவியல் முரண்பாடு என்றே அவர் கருதினார். ஆனால் இப்போது சந்திரசேகரின் ஆராய்ச்சி முடிவு, கருந்துளைகள் போன்ற அமைப்பு கட்டாயம் பிரபஞ்சத்தில் இருக்கும் என்று சொல்லுகிறதே. முடியாது! முடியவே முடியாது!! நிச்சயமாக, இதைப் போல விண்மீன்கள் முடிவிலியளவு சிறிதாக சுருங்குவதை தடுக்க இயற்கையில், இன்னும் நாம் கண்டுபிடிக்கப்படாத ஒரு விதி இருக்கும் என்று நம்பினார்.

பழைய தமிழ் பட வில்லன், நம்பியார் போல கையைப் பிசைந்துகொண்டே, “என்னடா சந்திரசேகரா, நான் என்ன செய்ய சொன்னா நீ என்ன செய்து வச்சிருக்கே?” என்று கேட்டது மட்டுமல்லாது, சந்திரசேகரின் ஆராச்சி துறையையே வேறு திசைக்கு மாற்றிவிட்டார். எடிங்க்டன் அப்போது மிகப் புகழ்பெற்ற ஒரு அறிவியலாளராக இருந்ததனால், சந்திரசேகரின் ஆராய்ச்சி முடிவில்  உடன்பட்ட பவுளி (Pauli), போர் (Bohr) போன்ற இயற்பியலாளர்களும் சந்திரசேகருக்கு சாதகமாக குரல்கொடுக்கவில்லை. அப்படி அவர்கள் குரல்கொடுத்திருந்தால், வரலாறு சற்றேமாறித்தான் போயிருக்கும்.

ரோபர்ட் ஓபன்கைமர்

சிறிது காலத்திற்கு சந்திரசேகரின் வரையறை மற்றும் அவரது ஆராய்ச்சி, இயற்பியல் சமூகத்தால் மறக்கப்படிருந்தாலும், 1939 களில் ரோபர்ட் ஓபன்கைமர் (Robert Oppenheimer) என்ற இயற்பியலாளர், அவர்தான் முதல் அணுகுண்டை உருவாகிய புண்ணியவான் (அனுகுண்டின் தந்தை என்றும் செல்லமாக அழைகிறார்கள்??!!), 1.4 சூரியத்திணிவை விட அதிகமாகவும், அதேவேளை 3 சூரியத்திணிவை விட குறைவாகவும் இருந்தால், அந்த விண்மீன் நியூட்ரான் விண்மீனாக மாறும் அதேவேளை, ஒரு விண்மீனின் மையப்பகுதியின் திணிவு 3 சூரியத் திணிவைவிட அதிகமாக இருப்பின், இயற்கையில் இருக்ககூடிய எந்தவொரு விதியும், அந்த விண்மீன் சுருங்கி கருந்துளையாவதை தடுக்கமுடியாது என நிறுவினார். அதுமட்டுமல்லாது, ஓபன்கைமருடன் அவரது சகாக்களும் சேர்ந்து சுவர்ட்சில்ட் ஆரை அளவுள்ள அளவிற்கு அந்த விண்மீன்கள் வரும்போது, அந்தக் கோளத்தினுள் துடிக்கும் நேரமும் நின்றுவிடும் என்றும் கூறினார். இதனால் அந்த விண்மீன்களுக்கு இவர்கள் “உறைந்த விண்மீன்கள்” என்று பெயரும் வைத்தனர்.

அது என்ன உறைந்த விண்மீன்கள்? அடுத்ததாக பார்ப்போம்.

நேரம் என்றால் என்னவென்று எப்போதாவது யோசித்துப் பார்த்ததுண்டா? சாதாரண வாழ்வில் எமக்கு நேரம் என்பது தொடர்ந்து துடித்துக் கொண்டிருக்கும் ஒரு வஸ்து! என்னதான் நடந்தாலும் நேரம் என்பது அதன் போக்கில் போய்கொண்டே இருக்கும். ஒவ்வொரு செக்கன்களும் கழிந்துகொண்டே இருக்கும். சென்ற நேரத்தை திரும்பி பெற முடியாதில்லையா?

ஐன்ஸ்டீனின் பொ.சா.கோ வெளிவரும் வரை அறிவியல், நேரத்தைப் பற்றி இப்படிதான் ஒரு கருத்தைக் கொண்டிருந்தது. குறிப்பாக நியூட்டன், நேரம் என்பது வில்லில் இருந்து புறப்பட்ட அம்பைப் போல அது தொடர்ந்து மாற்றமின்றி பயணிக்கும் என்றார். அவரைப் பொறுத்தவரை, நேரம் என்பது இந்த பிரபஞ்சம் எங்கும் ஒரேமாதிரியாக துடிக்கும் ஒரு விடயம். பூமியில் ஒரு செக்கன் என்பது, செவ்வாயிலும் ஒரு செக்கன், சூரியனிலும் ஒரு செக்கன், அதேபோல பிரபஞ்சத்திலுள்ள ஏனைய இடங்களிலும் ஒரு செக்கனே. வெளியை, சார்பானது என்று கருதிய நியூட்டன் நேரத்தை அறுதியானது என்றே கருதினார்.

ஆனால் ஐன்ஸ்டின் நேரத்தை ஆற்றில் பாயும் நீருக்கு ஒப்பிட்டார். ஆற்றில் இருக்கும் நீர் எப்படி, சிலவேளைகளில் வேகமாகவும், சிலவேளைகளில் மெதுவாகவும், சிலவேளைகளில் வளைந்து நெளிந்து போகுமோ, அதேபோல தான் நேரமும், வெளியும் என்றார் ஐன்ஸ்டின்.

ஐன்ஸ்டீனின் பொதுச் சார்புக் கோட்பாடு, நேரம், இடம், திணிவு மற்றும் வடிவியலை (geometry) தொடர்புபடுத்திக் கூறும் ஒரு கோட்பாடாகும். ஐன்ஸ்டீனின் இந்த கோட்பாடு, இடம் / வெளி(space), நேரம்(time) என்பவற்றை ஒரே வஸ்துவின் தொடர்ச்சி (continuum) என்று கூறுகிறது. அதாவது இந்த பிரபஞ்சத்தில் வெளியானது, முப்பரிமாணத்தால் ஆக்கப்பட்டுள்ளது – நீளம், அகலம் மற்றும் உயரம், இதைதான் நாம் x,y,z என ஆள்கூற்றுத் தளங்களில் குறிப்பிடுவோம். இத்தோடு, நேரத்தை நான்காவது பரிமாணமாக கொண்டு வெளிநேரம்(space-time) என்ற கணிதவியல் மாதிரியை உருவாக்கி, பல்வேறு பட்ட இயற்பியல் பிரச்சினைகளுக்கு ஐன்ஸ்டின் விடையளித்தார்.

அதில் மிக முக்கியமான ஒன்று, இந்த வெளி-நேரத்தில் ஏற்படும் வளைவுகளால் (curvature) உருவாக்கப்படும் ஒரு பக்கவிளைவே ஈர்ப்புவிசை ஆகும். இதை மாற்றி சொல்லவேண்டும் என்றால், திணிவானது வெளி-நேரத்தை வளைக்கவல்லது. வெளி-நேரத்தின் தொடர்ச்சியாகவும், நேரம், வெளியின் தொடர்ச்சியாகவும் இருப்பதனால் ஒரு இடத்தில் இருந்து இன்னுமொரு இடத்திற்கு எப்படியெல்லாம் பயணிக்க முடியுமோ, அதைப் போலவே, நேரத்திலும் பயணிக்க முடியும். ஒரு உதாரணத்தை பார்ப்போம்.

A என்ற இடத்தில் இருந்து B என்னும் இடம் ஒரு கிலோமீட்டர் தூரத்தில் இருக்கிறது என்று எடுத்துக்கொள்வோம். நாம் மணிக்கு 1 கிலோமீட்டர் வேகத்தில் நடந்தால் (அதாவது நத்தையை விட மெதுவாக!), ஒரு மணிநேரத்தில் அல்லது 60 நிமிடங்களில் A என்னும் இடத்தில் இருந்து B என்னும் இடத்தை அடைந்து விடுவோம். இதுவே மணிக்கு 10 கிலோமீட்டர் வேகத்தில் நடந்தால், 6 நிமிடந்த்தில் நாம் A யில் இருந்து B ஐ சென்றடைந்து விடுவோம் இல்லையா? இதே போலத்தான் நேரமும்! இரண்டு நேர இடைவெளிக்கு உள்ள இடைவெளி எப்போதுமே ஒன்றாக இருக்கவேண்டிய அவசியமில்லை. குழப்புகிறேனோ? தெளிவாக சொல்ல முயற்சிக்கிறேன்.

விளக்க முன் ஒன்றை சொல்லிக்கொள்ள விரும்புகிறேன். இனி நாம் பார்க்கப் போகும் கோட்பாடுகளும், இயற்கையின் விதிகளும், நமது சாதாரண போது அறிவை (common sense) அசைத்துப் பார்க்கப் கூடியவை. ஆகவே உங்களின் மூளையின் கற்பனைத்திறன் என்ற குதிரையை தட்டி சற்றே ஓட விடுங்கள். நான் சொல்லும் உதாரணங்களை ஒன்றுக்கு இரண்டு முறையாக அலசிப் பாருங்கள். அதுவும் முடியவில்லை என்றால் விட்டு விடுங்கள். டேக் இட் ஈசி.

நான் முன்னரே கூறியது போல, திணிவினால் வெளி-நேரத்தில் வளைவுகளை ஏற்படுத்த முடியும். இந்த வளைவுகளே ஈர்ப்பு விசை என்ற ஒன்று இருப்பது போன்ற மாயத் தோற்றத்தை உருவாகுகிறது. திணிவின் அளவு அதிகரிக்க அதிகரிக்க, அதைச்சுற்றியுள்ள வெளி-நேரத்தின் வளைவும் அதிகரிக்கும். எந்த அளவுக்கு வெளி-நேரம் வளைகிறதோ, அந்த அளவிற்கு வெளியும், நேரமும் வளையும். எந்தளவுக்கு வெளி-நேரம் வளைகிறதோ, அந்தளவிற்கு நேரமானது துடிக்கும் வீதமும் மாறுபடும்.

குறிப்பிட்ட புள்ளியில் திணிவு அதிகரிக்க அதிகரிக்க அது எவ்வாறு வெளிநேரத்தை வளைக்கிறது என்று இங்கே பார்க்கலாம்

இப்படி ஒரு உதாரணத்தை பாருங்கள், பூமியை விட சூரியன் 333,000 மடங்கு திணிவானது. ஆக, பூமியைச்சுற்றி வெளிநேரம் வளைந்துள்ளத்தை விட, சூரியனைச் சுற்றி வெளிநேரம் மிக அதிகமாக வளைந்துள்ளது. ஆகவே ஒரே நேரத்தை காட்டும் கடிகாரங்கள் இரண்டை தயாரித்து, ஒன்றை பூமியிலும், மற்றொன்றை சூரியனிலும் (அதில் வைக்கலாம் என்று எடுத்துக் கொள்வோம்) வைத்துவிட்டு, மீண்டும் சில காலத்தின் பின்னர் இரண்டு கடிகாரங்களையும் எடுத்து ஒப்பிட்டுப் பார்த்தால், சூரியனில் நாம் வைத்த கடிகாரத்தைக் காட்டிலும் பூமியில் இருந்த கடிகாரம் வேகமாக துடித்திருப்பது தெரியும். அதாவது, சூரியனது திணிவின் காரணமாக வெளி-நேரத்தில் ஏற்ப்பட்ட வளைவு, பூமியினால் ஏற்பட்ட வளைவைக் கட்டிலும் அதிகம் என்பதால், அது நேரத்தின் வேகத்தை, பூமியோடு ஒப்பிடும் போது குறைத்துள்ளது!  இதை ஈர்ப்புக்கால நேர நீட்டிப்பு (gravitational time dilation) என்று இயற்பியலாளர்கள் அழைகின்றனர்.

இன்னும் சுருங்கக் கூறின், ஈர்ப்புவிசை அதிகமாக இருக்கும் இடத்திற்கு அண்மையில் நேரம் மெதுவாகவும், ஈர்ப்புவிசை குறைந்த இடத்தில் நேரம் வேகமாகவும் துடிக்கும்.

ஐன்ஸ்டீனின் சிறப்புச் சார்புக் கோட்பாடு (special theory of relativity) மற்றும் பொதுச் சார்புக் கோட்பாடு (general theory of relativity) இந்த வேறுபாடுகளை அழகாக விளக்குகிறது. நமது நோக்கம் இங்கு கருந்துளைகள் பற்றி ஆராய்வதே என்பதால், அதோடு சம்பந்தப் பட்டவற்றை மட்டும் பார்க்கலாம், முடிந்தவரை அதோடு தொடர்புள்ளவற்றையும் விளக்குகிறேன்.

முன்னைய பகுதியல் கூறிய இந்த “உறைந்த விண்மீன்கள்” பற்றி இப்போது பார்க்கலாம், நாம் மேலே பார்த்த கருத்துக்களை இங்கே 3 சூரியத்திணிவை விட அதிகமாக இருக்கும் விண்மீன்களுக்குப் பொருத்திப் பார்கலாம்.

ஒரு விண்மீனின் மையப்பகுதியின் திணிவு 3 சூரியத் திணிவைவிட அதிகமாக இருப்பின், இயற்கையில் இருக்ககூடிய எந்தவொரு விதியும், அந்த விண்மீன் சுருங்கிக் கருந்துளையாவதை தடுக்கமுடியாது என ஓபன்கைமர் நிறுவிக்காட்டினார். அதுமட்டுமல்லாது, ஓபன்கைமருடன் அவரது சகாக்களும் சேர்ந்து சுவர்ட்சில்ட் ஆரை அளவுள்ள அளவிற்கு அந்த விண்மீன்கள் வரும்போது, அந்தக் கோளத்தினுள் துடிக்கும் நேரமும் நின்றுவிடும் என்றும் கூறினார். இதனால் அந்த நட்சத்திரங்களுக்கு இவர்கள் “உறைந்த நட்சத்திரங்கள்” என்று பெயரும் வைத்தனர்.

இப்படி இந்த சுவர்ட்சில்ட் ஆரை வரை வந்த விண்மீன்களானது மிக மிக அதிகளவான திணிவை ஒரு குறிப்பிட்ட கோள அளவினுள் (பந்து போல என்று நினைத்துக் கொள்ளுங்கள்) கொண்டிருக்கும். இது அந்த சுவர்ட்சில்ட் ஆரை கொண்ட கோளத்தினை சுற்றியுள்ள வெளிநேரத்தை மிக மிக அதிகளவாக வளைக்கிறது. எவ்வளவு தூரம் இப்படி வெளிநேரம் வளைகிறது என்றால், நேரம் துடிப்பதே நிற்கும் அளவிற்கு! சுவர்ட்சில்ட் ஆரையின் எல்லையில் நேரம் உறைகிறது. இதுவே ஓபன்கைமர் மற்றும் அவரது சகாக்கள் இந்த விண்மீன்களை “உறைந்த விண்மீன்கள்” என்று கூற வழிவகுத்தது.

இன்னும் சற்று தெளிவாக பார்க்கலாம். சுவர்ட்சில்ட் ஆரை கொண்ட விண்மீனை நோக்கி நாம் பயணிக்கிறோம் என்று வைத்துக் கொள்வோம். தூரத்தில் இருந்து எம்மை இன்னுமொருவரும் அவதானிக்கிறார். எம்மிடமும் ஒரு கடிகாரம் உண்டு, அவரிடமும் ஒரு கடிகாரம் உண்டு, அவரும் நாமும் புறப்படும் போது கடிகாரங்கள் ஒரே நேரத்தை காட்டுகின்றன. ஆனால் நாம் அந்த நட்சத்திரத்தை நெருங்க நெருங்க அவருக்கு எமது கடிகாரம் வேகம் குறைந்து செல்வதுபோல தோற்றம் அளிக்கும். (ஆனால் நமக்கு கடிகாரம் வேகம் குறைவது போல தென்படாது, காரணம், நேரம் என்பது அதை அளப்பவருக்கு சார்பானது, ஆகவே எமக்கு நேரத்தின் வேகம் குறைவது தெரியாமல் இருப்பதற்கு காரணம், நேரம் துடிப்பது என்பது கடிகாரத்துக்கு மட்டுமல்ல, எமது சிந்தனையின் வேகம், வயதாவதின் வேகம், கலங்கள் புதுப்பிக்கப் படுவதின் வேகம் என எல்லாமே நேரத்தால் மற்றமடைவதால், எமக்கு நேரம் மெதுவாக துடிப்பதின் வித்தியாசம் தெரியாது.)

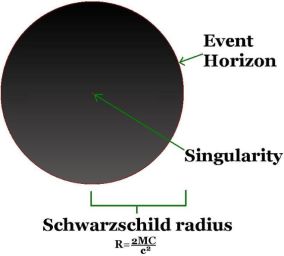
நாம் அப்படியே முன்னேறி, அந்த விண்மீனின் சுவர்ட்சில்ட் ஆரையை அடையும் போது, நாம் பூரணமாக உறைந்து விட்டது போலவே எம்மை அவதானித்துக் கொண்டிருபவருக்கு தெரியும். அவருக்கு நமது கடிகாரத்தின் முள் நின்றுவிட்டது போலவே தோன்றும். அவரைப் பொறுத்தவரை நாம் நேரம், காலம் என்ற ஒன்றில் இப்போது இல்லை. அவர் நம்மை இறுதியாக பார்த்தது, நாம் இந்த சுவர்ட்சில்ட் ஆரையை கடக்கும் போது தான். எம்மைப் பொறுத்தவரை, நேரம் ஓடிக்கொண்டே இருக்கும், நாம் சுவர்ட்சில்ட் ஆரையைக் கடந்து அந்த விண்மீனின் மையத்தை நோக்கி சென்றுகொண்டிருப்போம். அனால் நம்மால் இனி எப்போதுமே இந்த சுவர்ட்சில்ட் ஆரையை விட்டுவெளியே செல்ல முடியாது.

இதனால்த் தான் சுவர்ட்சில்ட் ஆரையை கொண்டுள்ள விண்மீனின் மேற்பரப்பை நிகழ்வெல்லை (event horizon) என்று அழைகின்றனர். இந்த நிகழ்வெல்லை, இடத்திற்கும், நேரத்திற்கும் ஒரு வேலிபோல செயற்படுகிறது. நிகழ்வெல்லைக்குள் அதாவது சுவர்ட்சில்ட் ஆரைக்குள் நடக்கும் எந்தவொரு நிகழ்வும் சுவர்ட்சில்ட் ஆரைக்கு வெளியே அல்லது நிகழ்வெல்லைக்கு வெளியே எந்தவொரு தாக்கத்தையும் ஏற்படுத்தாது.

ஒருவர் இந்த நிகழ்வெல்லைக்குள் விழுந்துவிட்டால், அவர் இந்த நிகழ்வெல்லையை கடக்கும் போதே, அவரை நிகழ்வெல்லைக்கு வெளியில் இருந்து பார்ப்பவருக்கு, நிகழ்வெல்லையை கடப்பவரது நேரம் துடிப்பது நின்றுவிடும். இனி அந்த நிகழ்வெல்லைக்குள் விழுந்தவரால் இந்தப் பிரபஞ்சத்தின் வெளிநேரத்தில் எந்தவொரு மாற்றத்தையும் ஏற்படுத்த முடியாது. அவர்தான் நேரத்துக்கும் அப்பார்ப்பட்ட ஒரு இடத்திற்கு சென்றுவிட்டாரே!

இந்த நிகழ்வெல்லைக்குள்ளே தான் கருந்துளை என்னும் இயற்கையின் இனம்புரியா விந்தை ஒன்று ஒழிந்துள்ளது. காலம், நேரம், இடம், வெளி என்பவற்றை கடந்து நிற்கும் இந்த இயற்கையின் விந்தை, நம் பிரபஞ்சத்தைப் பற்றிய அறிவியல் தேடலில் ஒரு தொடக்கமே!

அடுத்ததாக கருந்துளைகளை நோக்கி பயணிப்போம்.

சாதாரண வாழ்வில், இங்கு பூமியில், நாம் அனுபவிக்கும் அல்லது பார்க்கும் விடயங்கள் அனைத்தும் பிரபஞ்சத்தில் நடக்கக்கூடிய, அல்லது அனுபவிக்ககூடிய விடயங்களில் ஒரு துளியளவே. நாம் பிறந்ததிலிருந்தே இந்த பூமியில் வாழ்வதால் நமக்கு தெரிந்த அனைத்தும் “போது அறிவு” உட்பட, எல்லாமே நமது மூளையால் பூமியின் இடத்தில் இருந்தே ஒப்பிடப்படும். நமது சந்திரனைப் பொறுத்தவரை, அதன் ஈர்ப்பு விசையானது பூமியைப் போல ஆறில் ஒரு பங்கு மட்டுமே. அதாவது இங்கு ஒரு மீட்டார் துள்ளக்கூடிய ஒருவரால் சந்திரனில் 6 மீட்டர்கள் துள்ளலாம். கற்பனை செய்து பாருங்கள், 6 மீட்டர் உயரத்துக்கு ஒருவர் அசால்ட்டாக தாவினால் எப்படி இருக்கும். ஸ்பைடர்மேனே தோற்றுவிடுவார் போல! நம்மைப் பொறுத்தவரை அது ஒரு அதிசயம் போலத்தான் ஏனென்றால் பூமியில் அப்படி பாய்ந்த ஒருவரும் இல்லை. நமது அறிவு, பூமியை சார்ந்தே இருக்கிறது!

இந்த பரந்து விரிந்த பிரபஞ்சத்தில் ஒரு துளியை விட சிறிதாக இருக்கும் எம்மை விட பல்வேறுபட்ட வித்தியாசமான உண்மைகள்/நிகழ்வுகள் உண்டு. எமக்கு அது அதிசயமாக இருந்தாலும், இயற்கையைப் பொறுத்தவரை எல்லாமே ஒன்றுதான்! இப்படி இருக்கும் பல்வேறு வித்தியாசமான வஸ்துக்களில், எமது இயல்பறிவுக்கு மிக மிக தொலைவில் இருக்கும் ஒரு விடயம் தான் இந்த கருந்துளைகள்.

சென்ற பதிவுகளில் நாம் விரிவாக, நேரம், காலம், இடம், ஈர்ப்பு சக்தி என்பனவெல்லாம் எவ்வாறு இந்த பிரபஞ்சத்தில் வெவ்வேறு இடங்களில் வெவ்வேறு வீதங்களில் தாக்கம் செலுத்துகிறது என்று பார்த்தோம். அவை நமது வழமையான, காலம், நேரம், இடம் என்பவற்றைவிட வேறுபட்டு தெரிந்திருக்கலாம். இயற்கையின் விளையாட்டில் இதுவும் ஒன்று. சரி கருந்துளைகளைப் பற்றிப் பார்ப்போம்.

நாம் ஏற்கனவே பார்த்ததுபோல, விண்மீனின் மையப்பகுதி, 3 சூரியத் திணிவை விட அதிகமாக இருப்பின், விண்மீன் பெருவெடிப்பின் பின்னர் எஞ்சும் மையப் பகுதியானது தனது சொந்த ஈர்ப்புசக்தியால் சுருங்கிச் செல்வதை இயற்கையில் உள்ள எந்தவொரு சக்தியாலும் தடுக்க முடியாது. இப்படி சுருங்கி செல்லும் இந்த கோளவடிவான மையப்பகுதி ஒரு கட்டத்தில், சுவர்ட்சில்ட் ஆரை அளவுள்ள கோளமாக சுருங்கியவுடன், அங்கு கருந்துளை பிறக்கிறது.

கருந்துளைக்கு இவ்வாறு நாம் வரைவிலக்கணம் கூறலாம்.

வெளி-நேரத்தில் இருக்கும் ஒரு குறிப்பிட்ட இடம், இங்கு ஈர்ப்பு விசையின் அளவு மிக மிக அதிகமாக இருப்பதனால், ஒளியினால் கூட இவ்விடத்தில் இருந்து தப்பிக்க முடியாது. ஒளியை இங்கு குறிப்பிடக் காரணம், பிரபஞ்சத்தில் மிக மிக வேகமாக செல்லக்கூடியது ஒளிமட்டுமே, ஆக, அதனாலேயே இந்த கருந்துளையின் ஈர்ப்புவிசையில் இருந்து தப்பிக்க முடியாவிட்டால், பிரபஞ்சத்தில் உள்ள வேறு எதனாலும் தப்பிக்கமுடியாது! விண்மீன்களின் முடிவில் கருந்துளை ஒன்று பிறக்கலாம்.

கருந்துளையும் அதனைச் சுற்றியுள்ள பகுதிகளும் மிக அதிகமாக ஈர்ப்புவிசையை கொண்டிருப்பதனால், இவ்விடங்களில் இருக்கும் வெளி-நேரத்தின் பண்புகள் மிக மிக விசித்திரமாக இருக்கின்றன. இவற்றை கருத்தில் வைத்தே இந்த அளவுக்கு அதிகமான ஈர்ப்புவிசை கொண்ட பொருளை, “கருந்துளை” (Black hole) என முதன் முதலில் ஜான் வீலர் (John Wheeler) 1967 இல் அழைத்தார். அதுவே நல்ல கவர்சிகரமான பெயராக இருந்ததால், தொடர்ந்து அந்தப் பெயரே பிரபல்யமாகி விட்டது.

சுவர்ட்சில்ட் ஆரையில் என்னவிதமான மாற்றங்கள் இடம்பெறும் என்று நாம் ஏற்கனவே பார்த்து விட்டபடியால், நாம் மேற்கொண்டு கருந்துளைகளைகளின் இயல்புகளைப் பற்றிப் பார்க்கலாம்.

கருந்துளைகள் கருப்பா? ஒரு சின்ன கேள்வி தான்! கருந்துளைகள், விண்மீன்களைப் போல, ஒளியை வெளிவிடுவதில்லை ஆக, அவற்றை தொலைக்காட்டிகளை கொண்டு பார்க்கவோ, அறியவோ முடியாது. அவை கண்களுக்கு புலப்படாதவை. ஆனால் அவையென்றும் தங்களை முழுதாக மறைத்துக் கொள்ளவில்லை. இந்த கருந்துளைகளின் அளவுக்கதிகமான ஈர்ப்புவிசை, அதை சுற்றியுள்ள பொருட்களின் மீது செலுத்தும் செல்வாக்கை வைத்துக்கொண்டு எம்மால் இலகுவாக இந்த கருந்துளைகளை கண்டுகொள்ளமுடியும்.

எப்படி இந்த கருந்துளைகளை, வானியலாளர்கள் கருவிகளைக்கொண்டு அறிகிறார்கள் என்று பார்ப்போம்.

கருந்துளைகளை நேரடியாக அவதானிக்க முடியாவிட்டாலும், அதனருகில் உள்ள விண்மீன்களில் இருந்து வரும் ஒளி, எக்ஸ்-கதிர் மற்றும் ரேடியோ கதிர்களைக்கொண்டு அவதானிக்கும் வானியலாளர்கள், குறிப்பிட்ட விண்மீனின் வேகத்தை அளக்கின்றனர். பின்னர் இந்த வேகத்தை, ஈர்ப்புவிசை தொடர்பான சமன்படுகளோடு ஒப்பிட்டு பார்த்து, இந்த விண்மீனின் வேகத்தில் இருக்கும் மாறுதல்களுக்கான காரணத்தை கண்டறிகின்றனர். அதாவது, இந்த விண்மீன் ஒரு கருந்துளையை சுற்றி வருகிறது என்றால், இந்த விண்மீனின் வேகம் எவ்வாறு இருக்கும் என இந்த சமன்பாடுகள் நம்மக்கு சொல்கின்றன, இதை வைத்து குறிப்பிட்ட விண்மீன் ஒரு கருந்துளையை சுற்றி வருவத்தை வானியலாளர்களால் துல்லியமாக கூறமுடியும்.

அதுமட்டுமல்லாது, கருந்துளைகளை சுற்றி அளவுக்கதிகமான ஈர்ப்புவிசை இருப்பதனால், கருந்துளையின் ஈர்ப்பினால் அதனை நோக்கி வரும் பிரபஞ்ச தூசு துணிக்கைகள், வளைவுந்த்தின் காரணமாக கருந்துளையைச் சுற்றி ஒரு தட்டுப் போல ஒரு அமைப்பை (accretion disk) உருவாக்குகின்றது, இந்த துணிக்கைகள் மற்றும் வாயுக்களால் ஆன அமைப்பு மிக மிக வேகமாக சுழன்றுகொண்டே கருந்துளையை நோக்கி விழுவதால் உருவாகும் அழுத்த சக்தியால் இந்த துணிக்கைகளும் வாயுவும் அளவுக்கதிகமான வெப்பநிலையை அடைகின்றன. இப்படி கருந்துளையின் மேற்பரப்புக்கு அண்மைய பகுதியில் உருவாகும் அதிகூடிய வெப்பநிலை பெரும்பாலும் எக்ஸ்-கதிர்களாக வெளியிடப்படுகின்றன. இந்த எக்ஸ்-கதிர்களை அவதானிப்பதன் மூலமும் எம்மால் கருந்துளைகளை கண்டுகொள்ளமுடியும்.

கருந்துளையில் இருந்து வெளிவரும் எக்ஸ் கதிர்வீச்சு

சரி கருந்துளையின் பண்புகள் என்று பார்த்தால், ஒரு திடமான கருந்துளை ஒன்றுக்கு மூன்றுவிதமான அடிப்படை பண்புகள் உள்ளன.

1. திணிவு (mass)
2. மின் ஏற்றம் (electric charge)
3. சுழல் உந்தம் (angular momentum) – அதாவது எவ்வளவு வேகமாக கருந்துளை சுழல்கிறது என்று வைத்துக்கொள்ளலாம்.

ஒரு கருந்துளைக்கு இந்த மூன்று பண்புகள் மட்டுமே உண்டு என “முடியில்லாக் கோட்பாடு” (no-hair theorem) கூறுகிறது. அதாவது இதைத் தவிர மேலதிகமான பண்புகள் இந்த கருந்துளை உருவாகும் போது இருந்திருந்தாலும், இந்த வஸ்துக்கள் அனைத்தும் இப்போது இந்த கருந்துளையால் கபளீகரம் செய்யப்பட்டு விட்டதால், அதாவது கருந்துளையின் நிகழ்வு எல்லைக்குள் (event horizon) அவை சென்றுவிட்ட பின்னர், கருந்துளைக்கு வெளியில் இருக்கும் வெளி-நேரத்தில் அவை எந்தவிதமான செல்வாக்கும் செலுத்துவதில்லை. ஆக, இந்த மூன்று பண்புகள் மட்டுமே கருந்துளை ஒன்றுக்கு இருக்கக்கூடிய மற்றும் நாம் அவதானிக்கக்கூடிய பண்புகளாகும். எப்படி இருந்தாலும் இந்த முடியில்லாக் கோட்பாடு இன்னும் பூரணமாக கணித ரீதியாக நிருபிக்கப்படவில்லை. அதேபோல இது தவறு என்றும் ஒருவராலும் நிருபிக்கப்படவில்லை. ஆகவே இது கொஞ்சம் சிக்கலுக்குரிய விடயம் தான். இருந்தும் அதிகமான இயற்பியலாளர்களும், கணிதவியலாலர்களும் இந்த முடியில்லாக் கோட்பாடுக்கு ஆதரவாகவே இருக்கின்றனர்.

இந்தக் கோட்பாட்டின் படி, நாம் இரண்டு கருந்துளைகளை ஒப்பிட்டுப் பார்க்கும் போது, இரண்டும், ஒரே அளவான திணிவையும், ஒரே ஏற்றத்தையும் மற்றும் ஒரே மாதிரியான சுழல் உந்தத்தையும் கொண்டிருப்பின், அவை இரண்டும் ஒத்த கருந்துளைகள் எனப்படும் – அதாவது ட்வின்ஸ் என்று நினைத்துக்கொள்ளுங்கள். அவற்றை வேறுபடுத்தி பிரித்து இனங்கான முடியாது!

ஒரு பொருள் கருந்துளைக்குள் விழுந்தால் என்ன நடக்கும்? அந்தப் பொருளுக்கு என்ன மாற்றம் நடக்கும்? அந்தக் கருந்துளைக்கு என்ன மாற்றம் நடக்கும்? பார்க்கலாம்.

நாம் இதுவரை பார்த்த மாதிரிகளில், கருந்துளை ஒன்று விண்மீனின் முடிவில் உருவாகலாம் என்று பார்த்தோம். விண்மீன்களின் முடிவில் தான் ஒரு கருந்துளை உருவாகவேண்டும் என்று ஒரு விதியும் இல்லை, ஆனால் மிகத் திணிவான விண்மீனின் (சூரியனைப் போல 20 மடங்குக்கு மேல்) முடிவானது ஒரு கருந்துளை உருவாகுவதற்கு தேவையான காரணிகளை உருவாகுகிறது. சிலவேளைகளில், மிக மிக அடர்த்தியான பிரபஞ்ச வஸ்துக்கள், தங்களின் ஈர்ப்பு விசையால் நெருங்கி வரும் போது, அவற்றின் மொத்த திணிவினால் உருவாகிய ஈர்ப்புவிசை அந்த வஸ்துக்களால் கட்டுப்படுத்த முடியாவிடில், அவை சுருங்கத்தொடங்கி கருந்துளையாக மாற சந்தர்ப்பமும் உண்டு.

கருந்துளைகளைப் பொறுத்தவரை, அளவை அடிப்படையாக கொண்டு நாம் அவற்றை மூன்று வகையாக பிரிக்கலாம்.

1. விண்மீனளவு கருந்துளைகள் (stellar mass black holes)
2. மிகப்பாரிய கருந்துளைகள் (supermassive black holes)
3. நுண்ணிய கருந்துளைகள் (miniature black holes)

விண்மீனளவு கருந்துளைகள்

இவை சாதாரணமாக விண்மீன்களின் முடிவில் ஏற்படும் சூப்பர்நோவாவின் பின்னர் உருவாகும் கருந்துளைகள். இவை சூரியனைப்போல ஐந்து மடங்கு திணிவில் இருந்து ஐம்பது அல்லது நூறு மடங்குக்குள் திணிவுள்ளதாக இருக்கும். விண்மீன்களின் முடிவில் பிறக்கும் இந்த கருந்துளைகளைப் பற்றி நாம் நிறைய விடயங்களை தெரிந்து வைத்துள்ளோம்.

பொதுவாக இவ்வகையான கருந்துளைகளை அவதானிப்பது மிக மிக கடினம், அதிலும் தனியாக இருக்கும் வின்மீனளவு கருந்துளைகளை அவதானிப்பது என்பது குதிரைக்கொம்பு. ஆக நாம் கண்டுள்ள இந்த வகையான கருந்துளைகள் பெரும்பாலும் இரட்டை விண்மீன் தொகுதிகளில் இருப்பவையே.

இரட்டை விண்மீன் தொகுதி என்பது இரண்டு விண்மீன்கள் ஒன்றை ஒன்று சுற்றிவரும் அமைப்பாகும். சூரியனைப் பொறுத்தவரை அது தனிப்பட்ட விண்மீன், ஆனால் பிரபஞ்சத்தில் பெரும்பாலான விண்மீன்கள் இரட்டைத் தொகுதிகளாகவே காணப்படுகின்றன.

இப்படி இரண்டு விண்மீன்கள் ஒன்றை ஒன்று சுற்றிவரும்போது, ஒன்று கருந்துளையாகிவிட்டால், எம்மால் இதனை இலகுவாக கண்டுகொண்டுவிட முடியும். அதாவது இரண்டு விண்மீன்கள் ஒன்றை ஒன்று சுற்றுவது போல இருக்கும், ஆனால் தொலைக்காட்டி மூலம் அவதானிக்கும் போது, அங்கே ஒரே ஒரு விண்மீன் மட்டுமே தெரியும். எக்ஸ்கதிர் தொலைக்காட்டி மூலம், மற்றைய மறைந்துள்ள விண்மீன் இருக்கும் இடத்தை அவதானிக்கும் போது அங்கே ஒரு எக்ஸ்கதிர் முதல் ஒன்று இருப்பதை காணக்கூடியவாறு இருக்கும். இதன்மூலம் அந்த மற்றைய விண்மீன் ஒரு கருந்துளை என்பதனை அறிந்துகொள்ளலாம்.

ஆனால் அதிலும் ஒரு சிக்கல் உண்டு, பெரும்பாலும் மற்றைய விண்மீன் ஒரு நியூட்ரான் விண்மீனாகவும் இருக்கவும் வாய்ப்புக்கள் அதிகம். ஏனெனில் கருந்துளைகள் அல்லது நியூட்ரான் விண்மீன்கள் ஆகியவை உருவாகும் அடிப்படை ஒரே மாதிரி இருப்பதாலும், அதனைச் சுற்றி இயங்கும் அமைப்புக்கள் ஒரே மாதிரி இருப்பதும் மேலும் அவை ஒரேமாதிரியாக எக்ஸ்கதிர்களை வெளிவிடுவதாலும், மற்றும் இரண்டுமே மிக மிக சிரிதாக இருப்பதாலும் அதிகளவான ஈர்ப்புவிசையை தன்னைச் சுற்றியுள்ள வெளிநேரத்தில் செலுத்துவதால் இந்த குழப்பம் ஏற்படும்.

எப்படி இருப்பினும், கருந்துளையை விட, நியூட்ரான் விண்மீன்களுக்கு என்று சில தனிப்பட்ட பண்புகள் உண்டு.

முதலாவது, அளவுக்கதிகமான காந்தப்புலம், நாம் ஏற்கனவே அளவுக்கதிகமான காந்தப்புலத்தை நியூட்ரான் விண்மீன்கள் கொண்டுள்ளன என்று பார்த்துள்ளோம், அதிலும் மிகையான காந்தபுலம் கொண்ட நியூட்ரான் விண்மீன்கள் மக்னடார் எனப்படும் என்றும் பார்த்துள்ளோம்.

இரண்டாவது, இந்த நியூட்ரான் விண்மீன்கள் சுழலும்போது, அதன் பாகங்கள் வேறுபட்ட சுழற்சி வேகத்தை காட்டும், அதாவது துருவங்கள் குறிப்பிட்ட வேகத்திலும், மத்திய பகுதி இன்னுமொரு வேகத்திலும் சுழலும், இது differential rotation அல்லது வேறுபட்ட சுழற்சி (அல்லது வேறுபட்ட பகுதிச் சுழற்சி எனவும் அழைக்கலாம்) எனப்படும். (நமது சூரியன், வியாழன் மற்றும் சனியிலும் இந்த “வேறுபட்ட சுழற்சி” இடம்பெறுகிறது எனபது குறிப்பிடத்தக்கது.) ஆனால் கருந்துளையைப் பொறுத்தவரை இப்படிப்பட்ட வேறுபட்ட சுழற்சி இல்லை. கருந்துளைகளுக்கு வெறும் மூன்று பண்புகளே உள்ளன என முதலில் நாம் பார்த்தோம்.

இப்படிப்பட்ட பண்புகளை இந்த இரட்டை விண்மீன் தொகுதில் உள்ள அந்த மறைவான விண்மீன் காட்டும்போது, அது ஒரு நியூட்ரான் விண்மீன் என உறுதி செய்யப்படும், அப்படி இல்லையேல் அது ஒரு கருந்துளையே!

மிகப்பாரிய கருந்துளைகள்

இவை சூரியனைப் போல பல பில்லியன் மடங்கு திணிவானவை. விண்மீனளவு கருந்துளைகளைப் போல அல்லாது இவை விண்மீன் பேரடைகளின் மையங்களில் இருக்கின்றன.

பொதுவாக இந்த பாரிய கருந்துளைகள் எப்படி உருவாகின்றது என்று இன்றுவரை ஒரு திடமான ஆராய்ச்சி முடிவில்லை, ஆனால் பெரும்பாலான வானியலாளர்கள் பின்வரும் கருத்தை முன்வைகின்றனர்.

விண்மீன் பேரடையின் மையத்தில் தோன்றும் பெரியளவான விண்மீனளவு கருந்துளைகள், கொஞ்சம் கொஞ்சமாக தன்னைச் சுற்றிவரும் தூசுகள், வாயுக்கள் மற்றும் ஏனைய விண்மீன்கள் போன்றவற்றை விழுங்கி கொஞ்சம் கொஞ்சமாக பெரிதாகிக்கொண்டே வரும். அதுமட்டுமல்லாது, மற்றைய விண்மீனளவு  கருந்துளைகளுடன் ஒன்றிணைந்து ஒரு பெரிய கருந்துளையாக உருவெடுக்கும். இதைவிட வேறுபட்ட மாதிரிகளும் இந்த மிகப்பாரிய கருந்துளைகள் எவ்வாறு உருவாகின்றன என்று சொல்கின்றன.

நமது விண்மீன் பேரடையான பால்வீதியின் மையத்தில் தனுசு எ* (Sagittarius A*) எனப்படும் மிக அடர்த்தியான ரேடியோ முதலானது ஒரு கருந்துளையாக இருக்கும் என வானியலாளர்கள் கருதுகின்றனர். பூமியில் இருந்து 26,000 ஒளியாண்டுகள் தூரத்தில் இருக்கும் இதனது விட்டம் (diameter) 44 மில்லியன் கிலோமீட்டர்கள் ஆகும். இது நமது சூரியனைப் போல கிட்டத்தட்ட 4 மில்லியன் மடங்கு திணிவானது.

முக்கியமான விடயம் என்னவென்றால், இந்த தனுசு எ*, மிகப்பாரிய கருந்துளைகள் என்ற வகையினுள் இருக்கும் ஒரு சிறிய கருந்துளை, ஆம் மிகப்பாரிய கருந்துளை என்ற பெயருக்கே இழுக்கு வருமளவு சிறியது இது!

நமக்கு அருகில் இருக்கும் விண்மீன் பேரடைகளில் இருக்கும் மிகப்பாரிய கருந்துளைகளின் அளவுகளை வானியலாளர்கள் அளந்துள்ளனர், அவற்றைப் பற்றிப் பார்ப்போம்.

நமக்கு மிக அருகில் இருக்கும், அதாவது நமக்கு 2.5 மில்லியன் ஒளியாண்டுகள் தூரத்தில் இருக்கும் அன்றோமீடா பேரடையின் மையத்தில் இருக்கும் பாரிய கருந்துளையானது கிட்டத்தட்ட 150-250 மில்லியன் சூரியத்திணிவு அளவானது. பலே பாஸ்கரா! ஆனால் இதையும் விழுங்கிவிடும் அளவுக்கு மேலும் பெரிய கருந்துளைகள் உண்டு.

இங்கிருந்து 55 மில்லியன் ஒளியாண்டுகள் தொலைவில் இருக்கும் மெஸ்சியர் 87 எனப்படும் ஒரு பெரிய விண்மீன் பேரடையின் மையத்தில் இருக்கும் கருந்துளை, 6.4 பில்லியன் சூரியத் திணிவுள்ளது (6400 மில்லியன் சூரியத் திணிவு).

M87 – மஞ்சள் புள்ளி, அதன் மையத்தில் இருக்கும் கருந்துளையில் இருந்து வெளிவரும் ஜெட் போன்ற நீளமான பிளாஸ்மா, இது 5000 ஒளியாண்டுகள் நீளமானது

NGC 3842 என்னும் விண்மீன் பேரடையின் மத்தியில் இருக்கும் பாரிய கருந்துளை 9.7 பில்லியன் சூரியத்திணிவுள்ளது.

நாம் இதுவரை அவதானித்ததிலே, மிகப்பெரிய கருந்துளை S5 0014+81 என்ற குவஸார் எனப்படும் அமைப்பில் இருக்கிறது, இது கிட்டத்தட்ட 40 பில்லியன் சூரியத் திணிவுகளை கொண்டுள்ளதாக வானியலாளர்கள் கருதுகின்றனர். அப்படியென்றால் நம் சூரியனைப் போல 40 பில்லியன் மடங்கு திணிவானது. இந்தப் பிரபஞ்சம் கொஞ்சம் பெரிதுதான்!

S5 0014+81 எப்படி இருக்கும் என்று ஒரு கற்பனை

நுண்ணிய கருந்துளைகள்

இவை மிக மிக சிறிய, அதாவது அணுவைவிட சிறிய கருந்துளைகள். இன்றுவரை இவை எந்தவொரு ஆய்வின் மூலமும் நிருபிக்கப்படவில்லை. குவாண்டம் இயற்பியலின் அடிப்படையில் அனுமானிக்கப்பட்ட இந்தக் கருந்துளைகள், ப்ரோட்டான் அளவிருக்கலாம்.

நுண்ணிய கருந்துளைகள்

இந்தப் பிரபஞ்சம் 13.7 பில்லியன் வருடங்களுக்கு முன் பெருவெடிப்பில் உருவாகியபோது இருந்த அளவுக்கதிகமான வெப்பநிலையும் அழுத்தமும் இப்படியான கருந்துளைகளை உருவாக்கி இருக்கலாம்.

இன்றுவரை இவை இருப்பதற்கான எந்தவொரு சாட்சியங்களும் இல்லதாதிருந்தாலும், கூடிய விரைவிலேயே இந்தப் பிரச்சினைக்கு ஒரு தீர்வு வந்துவிடும் என இயற்பியலாளர்கள் கருதுகின்றனர்.

அதாவது, எம்மிடம் இருக்கும் LHC போன்ற அதி சக்திவாய்ந்த துணிக்கை முடுக்கிகளைப் (particle accelerators) பயன்படுத்தி, இப்படி நுண்ணிய கருந்துளைகள் இருக்கின்றனவா இல்லையா என்ற ஒரு தீர்கமான முடிவை இனி வரும் வருடங்களில் எப்படியும் தீர்மானித்துவிட முடியும்.

1970 களில் ஸ்டீபன் காவ்கிங் (Stephen Hawking) கருந்துளைகள் பற்றிய ஆராச்சியில் ஈடுபட்டு, கருந்துளைகள் ஒருவிதமான கதிர்வீச்சை வெளியிடும் என அறிவித்தார், இன்று அது ஹாவ்கிங் கதிர்வீச்சு என அழைக்கப்படுகிறது. இந்த நுண்ணிய கருந்துளைகளும் இவ்வாறான கதிவீச்சை வெளியிடவேண்டும். அது மட்டுமல்லாது, காவ்கிங், இப்படியான நுண்ணிய கருந்துளைகள், நமது பால்வீதியை சுற்றி நிறைய இருக்கவேண்டும் என்றும் தெரிவித்தார்.

ஆக, இந்த காவ்கிங் கதிர்வீச்சை தேடி ஆராய்வதன் மூலமும் இப்படியான நுண்ணிய கருந்துளைகள் இருக்குமா என எம்மால் அறிந்துகொள்ள முடியும்.

கவ்கிங் கதிர்வீச்சைப் பற்றி நாம் பின்பு இன்னும் தெளிவாக பார்க்கலாம். கவலை வேண்டாம்.

நாம் எப்படி இந்த கருந்துளைகள் அறிவியலாளர்கள் வகைப் படுத்தியுள்ளனர் என்று பர்ர்தோம். இதைத் தவிரவும், சுழலும் கருந்துளைகள், நிலையான கருந்துளைகள் என்றும் சில வகைகள் உண்டு.

கருந்துளைகளின் பண்புகளைப் பார்க்க முன்னர், அவற்றின் வகைகளைப் பார்க்கவேண்டியது கட்டாயம் என்பதனாலேயே நாம் இங்கு வகைகளைப் பற்றிப் பார்க்கிறோம். ஏனென்றால் இந்த வகைகளுக்கு ஏற்ப, கருந்துளைகளின் பண்புகள் மாறும், ஆக இனி இந்தப் பண்புகளைப் பற்றிப் பார்க்கும் போது உங்களுக்கு தெளிவாக எந்தக் கருந்துளைகளைப் பற்றி நான் குறிப்பிடுகின்றேன் என தெளிவாக விளங்கும்.

மேலும் பயணிப்போம் கருந்துளைகளை நோக்கி.

கருந்துளைகளில் சிறியது தொடக்கம் பெரியது வரை வேறுபடுத்தி அதன் பண்புகளைப் பற்றிப் பார்த்தோம். அதிலும் நுண்ணிய கருந்துளைகள் இன்னமும் கண்டறியப்படாதது. ஆனால் விண்மீனளவு கருந்துளைகளும், மிகப்பாரிய கருந்துளைகளும் இருப்பதற்கான ஆதாரங்கள் எம்மிடம் உண்டு. இந்த மிகப்பாரிய கருந்துளைகள் ஒரு விண்மீன்பேரடைக்கு ஒன்று என்ற வீதத்தில் காணப்படும். அதாவது பேரடையின் மையப்பகுதியில் இவை காணப்படும். ஆனால் விண்மீனளவு கருந்துளைகள் அப்படியல்ல.

நமது பால்வீதியைப் பொறுத்தவரை கிட்டத்தட்ட 200 பில்லியன் விண்மீன்கள் உண்டு. இவற்றில் ஆயிரத்துக்கு ஒன்று என்ற வீதத்தில் பாரிய விண்மீன்கள் உண்டு, அதாவது பால்வீதியில் இருக்கும் ஒவ்வொரு ஆயிரம் விண்மீன்களுக்கு ஒரு விண்மீன் சுப்பர்நோவாவாகி வெடிக்கும் போது கருந்துளையாகும் அளவுக்கு பெரிதாக இருக்கும். (சரியாக ஒவ்வொரு ஆயிரத்துக்கும் ஒரு விண்மீன் இப்படி பெரிதாக இருக்கவேண்டும் என்று இல்லை, இது ஒரு அவதானிப்பு கணக்கீடு மட்டுமே.) ஆக, 200 பில்லியன் விண்மீன்களுக்கு, கிட்டத்தட்ட 200 மில்லியன் கருந்துளைகளாக மாறக்கூடிய விண்மீன்கள் இருக்கவேண்டும்.

இங்கு மிக முக்கியமாக குறிப்பிடவேண்டிய விடயம் என்னவென்றால், பாரிய விண்மீன்கள், வேகமாக தனது எரிபொருளை முடித்துவிட்டு சுப்பர்நோவாவாக வெடித்துவிடும். நமது பால்வீதியின் வயது, அண்ணளவாக 13.2 பில்லியன் வருடங்கள். சூரியன் போன்ற சிறிய விண்மீன்களே பில்லியன் கணக்கான வருடங்கள் வாழ்க்கைக் காலத்தை கொண்டுள்ளன. ஆனால் இந்த பெரிய விண்மீன்கள் பெரும்பாலும் சில நூறு மில்லியன் வருடங்களே வாழும். ஆக இதனால் சொல்லிக் கொள்வது என்னவென்றால், நமது பால்வீதியில் இருக்கும் பெரிய விண்மீன்களில் 90% மேலானவை ஏற்கனவே கருந்துளையாகிவிட்டன! ஆகவே, நமது பால்வீதியில் அண்ணளவாக 180 மில்லியன் விண்மீனளவு கருந்துளைகள் உண்டு என்று கணக்கிட்டுள்ளனர்.

இவ்வளவு கருந்துளைகள் இருந்தால் பூமிக்கு ஆபத்து இல்லாமலா இருக்கும்? கவலை வேண்டாம், பூமிக்கு மிக அருகில் இருக்கும் கருந்துளையானது, பூமியில் இருந்து 1600 ஒளியாண்டுகள் தூரத்தில் இருக்கிறது என்று 1999 இல் வானவியலாளர்கள் கண்டறிந்தனர்! கொஞ்சம் விசித்திரமான பெயர்தான் இதற்கு – V4641 சஜிட்டாரி (Sajittarii). இது ஒரு இரட்டை விண்மீன் தொகுதியில் இருக்கும் கருந்துளை அதனால் தான் இதை நம்மால் கண்டுகொள்ள கூடியதாக இருந்தது. அதாவது இந்த கருந்துளை, அதனருகே சுற்றிவரும் விண்மீனைக் கொஞ்சம் கொஞ்சமாக உறிஞ்சிக்கொண்டு இருக்கிறது. இப்படி உறிஞ்சுவதால் உருவாகும் எக்ஸ்கதிவீச்சை பூமியில் இருந்து வானவியலாளர்களால் அவதானிக்கக்கூடியதாக இருந்தது. இந்த கதிர்வீச்சில் இருந்து இந்த இடத்தில் ஒரு கருந்துளையும் இருக்கிறது என்று வானியலாளர்கள் கணித்தனர்.

ஆனால் இது எவ்வளவு தொலைவில் இருக்கிறது என்று மீண்டும் 2001 இல் கணக்கிட்ட வானியலாளர்கள், முதலில் கூறியதைவிட 15 மடங்கு தொலைவில் இந்த கருந்துளை இருப்பதாக இறுதியாக முடிவுக்கு வந்தனர், அதாவது 24000 ஒளியாண்டுகள். இவ்வளவு தூரத்தில் இருக்கும் கருந்துளையால் நமக்கு எந்தப் பாதிப்பும் வரப்போவதில்லை. ஆகவே நாம் பயப்படவேண்டியதில்லை. இருப்பினும் சிலபல சிக்கல்கள் இருக்கத்தான் செய்கிறது.

உதாரணமாக, எம்மால் நேரடியாக கருந்துளைகளை அவதானிக்க முடியாது. நமக்கு தெரிந்த இயற்பியல் விதிகள், கருந்துளைகளை சுற்றி இருக்கும் வாயுக்களையும் தூசுகளையும் எப்படி தன்னை நோக்கி கவரும் என நமக்கு சொல்கின்றன. இந்த செயற்பாட்டின் போது உருவாகும் கதிர்வீச்சுக்கள் எப்படிப் பட்டவை என்பதையும் இந்த இயற்பியல் விதிகள் சொல்கின்றன. ஆக, கருந்துளையை சுற்றி நடைபெறும் செயற்பாட்டை வைத்தே அங்கு கருந்துளை இருப்பதை எம்மால் ஊகிக்க முடியும்.

இரட்டை விண்மீன் தொகுதியில் ஒரு கருந்துளைக்கு மிக அருகில் மற்றைய விண்மீன் இருப்பதால், அதனில் இருக்கும் வாயுவை இந்த கருந்துளை உறிஞ்சி எக்ஸ்-கதிர்வீச்சை வெளியிடும், ஆகவே இவற்றை எம்மால் கண்டு பிடிப்பது சற்று இலகுவான காரியம். ஆனால் தனியாக ஒரு கருந்துளை இருந்தால், அதாவது அது சாப்பிடுவதற்கு அதனைச்சுற்றி வாயுக்களும் தூசுகளும் இல்லாவிடில், இருட்டில் வந்த கறுப்புப் பூனைபோல ஆகிவிடும் இந்தக் கருந்துளை. இதனைக் கண்டுபிடிப்பது என்பது குதிரைக் கொம்பே!

ஆக இப்படி தனியான கருந்துளைகள், நமது சூரியத் தொகுதிக்கு அருகில் இருந்தால் இவற்றை நாம் கண்டுபிடிக்க தவறிவிட மிக அதிகமான வாய்ப்புக்கள் உண்டு. ஆனாலும் பூமிக்கு ஆபத்து விளைவிக்கும் அளவுக்கு அருகில் எந்தவொரு கருந்துளையும் இல்லை என நம்மால் உறுதியாக கூறமுடியும். பூமி என்று இல்லாமல், நமது சூரியத் தொகுதிக்கே ஆபத்து விளைவிக்கும் அளவில் எந்தவொரு கருந்துளையும் அருகில் இல்லை. அப்படி இருந்தால் நிச்சயம் அதன் ஈர்ப்பு விசை நமது சூரியத் தொகுதியில் சிறிய மாற்றத்தை ஏற்படுத்தி இருக்கும். அப்படி ஒரு மாற்றத்தை நாம் இன்றுவரை அளக்கவில்லை. ஆக இப்போது நீங்கள் ஆழமாக மூச்செடுத்துக் கொள்ளலாம். ஆபத்து இல்லை.

இன்னுமொரு மிக முக்கியமான விடயம், கருந்துளைகள் எதோ அரக்கனைபோல பிரபஞ்சத்தில் பயணித்து, ஒவ்வொரு விண்மீனாக கபளீகரம் செய்து தனது வயிற்ரை நிரப்பும் ஒரு உயிரினம் அல்ல. ஒரு விண்மீன் எப்படியோ அதேபோல்தான் இந்த கருந்துளைகளும். ஒரேயொரு வித்தியாசம், கருந்துளைகள் மிக அதிகமான ஈர்ர்புவிசையை கொண்டன.

நமது சூரியன் இந்த பால்வீதியில் எப்படி பயனிக்கிறதோ, அதேபோல விண்மீன்களாக இருந்து கருந்துளையாக மாறிய விண்மீன்களும் அப்படியே பயணிக்கும். ஒரு விண்மீனைக் கோள்கள் சுற்றுவதுபோல, கருந்துளைகளையும் கோள்கள் அல்லது வேறு பொருட்கள், உதாரணமாக அதை ஆய்வு செய்ய சென்ற விண்கலம் சுற்றிவரலாம்.

சூரியனானது நம் பூமியை அதனை நோக்கி இழுத்துக்கொண்டே இருக்கிறது, அதாவது வானில் எறிந்த பந்து மீண்டும் நிலத்தை நோக்கி வருவதுபோல பூமியும் சூரியனை நோக்கி விழுந்துகொண்டே இருக்கிறது. ஆனால் சூரியனில் போய் முட்டிவிடாமல் தடுப்பது இந்த பூமியின் வேகம். பூமியானது சூரியனை ஒரு செக்கனுக்கு 30 கிலோமீட்டர்கள் என்ற வேகத்தில் சுற்றி பயணிக்கிறது. இதனால் சூரியனின் ஈர்ப்பால் பூமி சூரியனை நோக்கி செல்வதற்குள், வேறு இடத்திற்கு சென்றுவிடும், இப்படி தொடர்ச்சியாக நடைபெறுவதால் பூமி தொடர்ந்து சூரியனை நீள்வட்டப் பாதையில் சுற்றிவருகிறது.

இது ஒரு அழகான காதல் கதை, இயற்கையின் காதல் கதை. சூரியன் தனது ஈர்ப்பால் பூமியை இழுத்துக் கொண்டே இருக்கும், பூமியும் சூரியனை நோக்கி விழுந்துகொண்டே இருக்கும், ஆனால் பூமி வேகமாக பயணிப்பதால், சூரியனை நோக்கி விழுவதற்கு முன் அதன் திசை மாறிவிடும், இது அப்படியே சூரியனை பூமி தொடர்ந்து சுற்றிவர காரணமாகிறது. இதேபோலத்தான் நம் சந்திரனும் பூமியை நோக்கி விழுந்துகொண்டே இருக்கிறது ஆனால் சந்திரனின் வேகம் அதிகமாக இருப்பதால் அது பூமியை சுற்றிவருமாறு ஆகிவிட்டது.

இங்கு மிக முக்கியமாக கவனிக்க வேண்டிய விடயம், ஒருவேளை சூரியனை சுற்றிவரும் பூமியின் வேகம் குறைவாக இருந்தால், சூரியனை சுற்றத் தொடங்கிய பூமி கொஞ்சம் கொஞ்சமாக தனது பாதையை சுருக்கிக் கொண்டு (அதன் பதை ஒரு சுழல் போல தெரியும்) சூரியனில் சென்று மோதிவிடும்.

இதுவே பூமியின் வேகம் மிக அதிகமாக இருந்தால், சூரியனது ஈர்ப்பு விசை பூமியின் வேகத்துக்கு ஈடுகொடுக்கமுடியாமல், பூமியானது சூரியனை நோக்கி வளைவாக பயணித்து அப்படியே சூரியனது ஈர்ப்பை விட்டு வெளியே சென்றுவிடும்.

இதே போலத்தான் கருந்துளையும், அதனை நாமும் சுற்றிவர முடியும். நமக்கு தேவை அதனைச் சுற்றிவர தேவையான சரியான, துல்லியமான வேகம்.

கருந்துளையை மெதுவாக சுற்றத்தொடங்கினால், சுழல்போல பாதையில் சென்று கருந்துளையில் மோதிவிடுவோம்.

அதேபோல மிக அதிகமான வேகத்தில் சென்றால், கருந்துளையின் ஈர்ப்பில் இருந்து விடுபட்டு அப்படியே சென்றுவிடுவோம்.

ஒரு குறிப்பிட்ட நடுத்தரமான வேகத்தில் பயணித்தால், எம்மால் கருந்துளையை சுற்றிவரமுடியும் ஆனால் அந்த பாதை வெறும் வட்டமாகவோ, நீள்வட்டமாகவோ இருக்காது. அது பார்ப்பதற்கு மிக சிக்கலான ஒரு பாதையாக இருக்கும்.

ஒரு குறிப்பிட்ட கருந்துளையை சுற்றிவர ஒரே ஒரு குறிப்பிட்ட வேகம் மட்டுமே உண்டு. அந்த வேகத்தில் பயணித்தால் நிச்சயம் எம்மால் கருந்துளையை வட்டப் பாதையில் சுற்றிவரமுடியும். ஆனால் அந்தப் பாதையிலோ வேகத்திலோ சிறிய மாற்றம் ஏற்பட்டாலும், ஒன்று நாம் கருந்துளைக்குள் சென்று மோதிவிடலாம், சற்று அதிர்ஷ்டம் இருந்தால், கருந்துளையின் ஈர்ப்பில் இருந்துவிடுபட்டு கருந்துளையை விட்டு சென்றுவிடலாம்.

கருந்துளைகளைப் பற்றி நிறைய விடயங்களை பார்த்துவிட்டோம். சில பல கேள்விகளுக்கு பதில்களைப் பார்க்கலாம். கருந்துளைகளை நம்மால் சுற்றிவரமுடியும் என்று பார்த்தோம். இப்போது கொஞ்சம் வித்தியாசமாக ஒன்றைப் பார்போம்.

ஒளி எப்போதும் நேர்கோட்டில் பயணிக்கும் என்று நாம் படித்திருப்போம். அது உண்மைதான். ஆனால் நேர்கோடு என்றால் என்ன என்ற கேள்விக்கு நாம் சுருக்கமாக, இரண்டு புள்ளிகளுக்கு இடையில் உள்ள மிகக் குறுகிய தூரம் என்று எடுத்துக் கொள்ளலாம். ஆனால் ஒரு பிரச்சினை என்னவென்றால் இந்த இரண்டு புள்ளிகளுக்கு இடையில் உள்ள தூரத்தை இணைக்கும் பாதை நேர்கோட்டுப் பாதையாக இருக்கவேண்டும் என்று எந்தவொரு கட்டாயமும் இல்லை. குழப்பமாக இருக்கலாம், விளக்குகிறேன்.

சிறிய பரிசோதனையை செய்து நாம் இந்த குழப்பத்திற்கான முடிவை அடையலாம். ஒரு A4 வெள்ளைக் கடதாசியை எடுத்துக் கொள்ளுங்கள். அதில் குறுக்காக ஒரு நேர்கோட்டை வரைந்துகொள்ளுங்கள். இப்போது கடதாசியை மேசையில் வைத்துவிடுங்கள். இப்போது கடதாசியில் ஒரு நேர்கோடு ஒன்று இருக்கும் அப்படித்தானே?

சரி, இப்போது இந்த கடதாசியை எடுத்து அந்தக் கோட்டின் இரு முனைகளும் சந்திக்குமாறு சுற்றிக் கொள்ளுங்கள். இப்போது அந்தக் கடதாசி வளைந்துள்ளது. அந்தக் கடதாசியில் வரைந்துள்ள கோடு நேர்கோடாக இருந்தாலும், கடதாசியே வளைந்திருப்பதால், அந்தக் கோடும் வளைந்திருக்கிறது. இங்கு நாம் இரு பரிமாணத்தில் (கடதாசியின் மேற்பரப்பு – இருபரிமாணப் பரப்பு) கோடு வரைந்துள்ளோம். அந்தக் கோடுதான் ஒளி செல்லும் பாதை என்று கொண்டால், கடதாசிதான் வெளி (space). இயற்கையில் இது முப்பரிமாண வெளியில் நடைபெறுகிறது.

நாம் ஏற்கனவே ஈர்ப்புவிசை வெளிநேரத்தை வளைக்கும் என்று பார்த்துள்ளோம். ஆனால் நாம் முன்பு, வெளிநேரத்தில் (space-time), இந்த ஈர்ப்புவிசை எப்படி நேரத்தில் செல்வாக்கு செலுத்துகிறது என்றே பார்த்துள்ளோம். இப்போது இது எப்படி வெளியில் செல்வாக்கு செலுத்துகிறது என்று பார்க்கப் போகிறோம். இயற்பியலில், வெளிநேரம் என்று சேர்த்து அழைப்பதற்கு காரணமே இவை இரண்டும் வேறு வேறு அல்ல என்பதால் ஆகும்.

எப்படி ஈர்ப்பு அதிகமுள்ள இடத்தில் நேரம் துடிக்கும் வேகம் குறைகிறதோ, அதேபோல ஈர்ப்பு அதிகமுள்ள இடத்தில் வெளியும் மிக அதிகமாக வளைகிறது. ஆம்! வெளியை ஈர்ப்பினால் வளைக்க முடியும்.

இந்தத் தொடரின் முடிவில், கருந்துளையைப் பற்றி நீங்கள் வியந்ததை விட ஈர்ப்பு விசை எப்படி இந்த பிரபஞ்சத்தை ஆளுகிறது என்றே வியப்படைவீர்கள். இந்தப் பிரபஞ்சத்தின் உண்மையான ஹீரோ, ஈர்ப்பு விசை தான். கருந்துளை என்பது, ஈர்ப்பு விசையின் பல்வேறு முகமூடிகளில் ஒன்று மட்டுமே! சரி மீண்டும் விடயத்துக்குள் சென்றுவிடுவோம்.

ஈர்ப்பு விசை கொண்ட அனைத்துப் பொருட்களுமே அதனைச் சுற்றியுள்ள வெளியை வளைக்கிறது. குறிப்பிட்ட பொருட்களின் திணிவிற்கு ஏற்ப இந்த வளைவின் அளவு மாறுபடுகிறது. குறிப்பாக கருந்துளைகளின் ஈர்ப்பு விசை மிக அதிகமாக இருப்பதால், கருந்துளையை சுற்றி வெளியானது மிக அதிகமாகவே வளைகிறது.

சூப்பர் ஜீனியஸ் ஐன்ஸ்டீன் தான் இந்த விளைவைப் பற்றிக் கூறியவர். அவரது பொதுச் சார்புக் கோட்பாடு, இந்த ஈர்ப்பு விசை என்பதே, திணிவானது (mass) அதனைச் சுற்றியுள்ள வெளிநேரத்தை வளைப்பதால் உருவாகும் ஒரு தோற்றம் என்கிறது.

நமது சூரியனை எடுத்துக் கொள்ளுங்கள். அது மிகத் திணிவான ஒரு பொருள். ஆகவே அது தன்னைச் சுற்றியுள்ள வெளியை வளைத்து வைத்துள்ளது. கோள்கள் எல்லாம் உண்மையில் நேர்கோட்டில் தான் பயணிக்கின்றன. ஆனால் அந்தக் கோடே, அதாவது அந்த நேர்கோட்டுப் பாதையே சூரியனது ஈர்ப்பினால் வளைக்கப் பட்டுள்ளதால் கோள்கள் சூரியனைச் சுற்றி வருகின்றன. அதாவது அந்த A4 கடதாசியை நீங்கள் முதலில் வளைத்தது போல.

திணிவானது எப்படி அதனைச் சுற்றியுள்ள வெளியை வளைகிறது என்று மேலுள்ள வீடியோவில் பார்க்கலாம்.

இன்னுமொரு உதாரணம் மூலம் விளக்குகிறேன். ஒரு சைக்கில் டயரை எடுத்துக் கொள்ளுங்கள். அந்த வெறும் டயரில் ஒரு சிறிய கல்லைப் போட்டு, இப்போது இந்த டயரை வேகமாக சுழற்றினால், அந்தக் கல்லானது அந்த டயரினுள்ளே சுழன்றுகொண்டு இருக்கும். அந்தக் கல்லைப் பொறுத்தவரை அது நேர்கோட்டில் தான் செல்லுகிறது, ஆனால் இந்த டயர் வளைந்து இருப்பதனால், அது வட்டப் பாதையில் செல்வதுபோல நமக்கு தோன்றும். அவ்வளவும்தான்!

இங்கு நாம் கவனிக்கவேண்டியது, ஒளியும் இந்த வெளியில் பயணிக்கும் ஒரு வஸ்துவே! ஆகவே, வெளிநேரமானது வளைந்திருக்கும் பட்சத்தில், அதில் பயணிக்கும் ஒளியும் வளைந்துதான் பயணிக்கும். ஒளியை ஈர்ப்புவிசை வளைக்கிறது என்று கருதுவதை விட பின்வருமாறு இலகுவில் விளங்கிக் கொள்ளுமாறு எடுத்துக் கொள்ளலாம்.

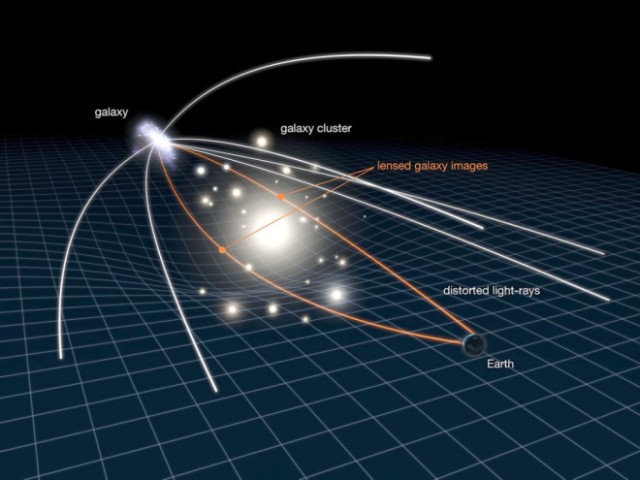
திணிவு அதிகமான பொருட்கள், தன்னைச் சுற்றியுள்ள வெளியை வளைக்கிறது, வெளியே வளைந்திருப்பதனால், அதில் பயணிக்கும் ஒளியும் வளைந்து செல்கிறது.

இப்படி ஒளி வளைவதை ஈர்ப்பு வில்லை (gravitational lensing) என்று அழைகின்றனர். அதாவது ஒரு ஒளிமுதலில் (light source) இருந்து வரும் ஒளியை எப்படி ஒரு வில்லை (lens) வளைக்குமோ, அதேபோல நட்சத்திரங்களில் இருந்து எம்மை நோக்கி ஒளி வரும்போது, குறிப்பிட்ட நட்சத்திரத்திற்கும் எமக்கும் இடையில் ஈர்ப்புவிசை அதிகமான ஒரு பொருள், அதாவது விண்மீன் பேரடை அல்லது கருந்துளை வரும் போது, குறிப்பிட்ட விண்மீனில் இருந்துவரும் ஒளியானது எப்படி ஒரு வில்லையினூடாக செல்லும்போது வளையுமோ அதேபோல இந்த ஈர்ப்பு விசை அதிகமான பொருளும் இந்த விண்மீன் ஒளியை வளைக்கும்.

நமக்கும், ஒரு விண்மீன் பேரடைக்கும் இடையில் கருந்துளை ஒன்று வரும்போது, அது எப்படி ஒளியை வளைகிறது என்று இங்கே பார்க்கலாம்

இப்படி ஈர்ப்புவில்லை மூலமாக வளைக்கப்பட்ட ஒளியானது பூமியை வந்தடையும் போது, அதை தொலைநோக்கி மூலம் பார்க்கும் ஒருவருக்கு, சற்று விசித்திரமான வகையில் அந்த குறிப்பிட்ட விண்மீன் தெரியும்.

சிலவேளைகளில் ஒரே விண்மீன் அல்லது வேறு ஒளிமுதல் ஒன்றுக்கு மேற்பட்ட இடங்களில் தெரியும். சிலவேளைகளில், ஈர்ப்பு வில்லையாக செயற்பட்ட வின்மீன்பேரடையை சுற்றி ஒரு வளையம் போலவும் தெரியலாம். இது குறிப்பிட்ட ஒளிமுதல், ஈர்ப்பு வில்லை மற்றும் அவதானிப்பவரின் அமைவிடத்தைப் பொறுத்து மாறுபடும்.

கருந்துளைகள் மிக மிக அதிகளவான ஈர்ப்புவிசைக் கொண்டுள்ளதால், கருந்துளையைச் சுற்றியுள்ள பகுதியில் இந்த ஈர்ப்பு வில்லைச் செயற்பாடு மிக அதிகமாக ஒளியை வளைக்கிறது. இப்படி வளைவது மட்டுமின்றி, கருந்துளைக்கு மிக அருகில் வரும் ஒளியானது, ஒரு கோள், எப்படி விண்மீனைச் சுற்றிவருமோ அதேபோல கருந்துளையையும் சுற்றுகிறது – காரணம், அந்தளவுக்கு கருந்துளை தன்னைச் சுற்றியுள்ள வேளிநேரத்தை வளைத்துள்ளது.

ஐன்ஸ்டீன் சிலுவை எனப்படும் இந்த நான்கு நீல நிற புள்ளிகள், உண்மையிலேயே ஒரே ஒரு குவேசார் ஆகும். இந்த குவேசாருக்கு முன்னுள்ள விண்மீன் பேரடையால் இது நான்கு வெவேறு நட்சத்திரங்கள் போல தெரிகிறது.

நமது சூரியனும் இப்படி ஒளியை சற்று வளைப்பதை நாம் அவதானித்துள்ளோம். பூமியில் இருந்து சில பல பில்லியன் ஒளியாண்டுகள் தூரத்தில் இருக்கும் சில விண்மீன் பேரடைகள் சற்று அதிகமாகவே ஒளியை வளைப்பதைக் கூட நாம் அவதானித்துள்ளோம். ஆனால் இதுவரை கருந்துளைக்கு அருகில் இப்படியான ஈர்ப்பு வில்லை செயற்பாட்டின் மூலம் ஒளியானது வளைவதை நாம் நேரடியாக அவதானிக்கவோ இல்லை அதை புகைப்படம் எடுக்கவோ இல்லை. அதற்கு காரணம் நாம் இதுவரை அவதானித்த கருந்துளைகள் மிக மிகத் தொலைவில் இருப்பது, நமது தற்போதைய தொலைக்காடிகள் அவ்வளவு தொலைவில் இருக்கும் கருந்துளைகளை அவ்வளவு தெளிவாக காட்டக் கூடியளவு சக்திவாய்ந்தவை அல்ல என்பதே.

கருந்துளையைச் சுற்றி ஒளியானது வளைந்துள்ள விதத்தை இப்படம் (CGI) காட்டுகிறது

இனிவரும் காலங்களில் நாம் தொழில்நுட்பத்தில் வளர்ந்து, அதன்பலனாக இப்படியான கருந்துளையைச் சுற்றி நடக்கும் ஈர்ப்பு வில்லை செயற்பாட்டை அவதானிக்கக்கூடியதாக இருக்கும் என வானவியலாளர்கள் கருதுகின்றனர்.

இந்த பிரபஞ்சத்தில் இருக்கும் எல்லாமே வெளிநேரத்தில் தான் அமைந்துள்ளது. வெளிநேரம் என்ற ஒன்றே இந்த பிரபஞ்சம் என நாம் கருதலாம். அதாவது வெள்ளை கான்வஸில் ஓவியம் வரைவதுபோல; இந்த கன்வாஸ் தான் வெளிநேரம், அதில் உள்ள ஓவியம் இந்த பிரபஞ்சத்தில் இருக்கும் அனைத்துப் பொருட்களும். நான், நீங்கள், உங்கள் வீட்டு டோமி நாய்க் குட்டி, உலகம், சூரியன், விண்மீன்கள், விண்மீன் பேரடைகள், கருந்துளைகள் என எல்லாமே இந்த ஓவியத்தில் இருப்பவையே! சரி குழப்பாமல் விடயத்திற்கு வருகிறேன்.

இந்த கருந்துளைகளைப் பொறுத்தவரை, நாம் ஏற்கனவே நாம் பார்த்த வரை, வெளிநேரம் என்ற ஒன்றை அது அளவுக்கதிகமாக இழுத்து வளைக்கிறது. நிகழ்வெல்லை (even horizon) என்ற ஒன்றைப் பற்றி நாம் ஏற்கனவே பார்த்துள்ளோம். இந்த நிகழ்வெல்லையை நாம் கருந்துளையின் எல்லை என்றும் அழைக்கலாம். அதாவது இந்த நிகழ்வெல்லையிலே தான் கருந்துளையின் உட்பகுதி ஆரம்பமாகிறது. அதாவது இந்த நிகழ்வெல்லையில் ஈர்ப்பு விசை அதிகரித்து, அந்தப் பகுதியின் விடுபடு திசைவேகம் ஒளியின் வேகத்தை அடைகிறது, ஆக இந்த நிகழ்வெல்லைக்குள் இருந்து எதுவும் வெளிவர முடியாது. (பொதுச் சார்புக் கோட்பாட்டுப் படி எதுவும் ஒளியைவிட வேகமாக பயணிக்க முடியாதே!).

இந்த நிகழ்வெல்லையை நோக்கி நாம் செல்லும் போது, நம்மை அவதானித்துக் கொண்டு இருப்பவருக்கு, நாம் எதோ ஸ்லொவ் மோசன் படத்தில் வருவது போல தெரியும், நாம் கருந்துளையை நெருங்க நெருங்க, நமது இயக்க வேகம் குறைவது போல தெரியும், அதேவேளை நாம் பார்க்க சிவப்பாகிக் கொண்டே வருவோம். அதற்கும் காரணம் உண்டு.

கருந்துளையை நெருங்க நெருங்க, அது வெளிநேரத்தை இழுக்கும் அளவும் அதிகரிக்கும். அபோது இதில் பயணிக்கும் ஒளியும் விரிவடையும். ஒரு ஸ்ப்ரிங்கை இருகைகளிலும் பிடித்து இழுப்பதைப் போல சிந்தித்துப் பாருங்கள். ஒளியும் ஒரு மின்காந்த அலைதான். அதுவும், நாம் பார்க்கும் நிறங்கள், அதாவது வானவில்லில் தெரியுமே எழு நிறங்கள், அவை இந்த அலைவடிவத்தில் தான் இருக்கிறது. அலைகளுக்கு அலைநீளம் என்று ஒன்று உண்டு. இதையும் இலகுவில் விளங்க வேண்டும் என்றால், கடலில் பார்க்கும் அலைகளை நினைத்துக் கொள்ளுங்கள். இப்போது ஒரு சந்தர்ப்பத்தில் 2 செக்கன் இடைவெளியில் இரண்டு அலைகள் வருகிறது என்று வைத்துக் கொள்வோம். பிறகு சிறிது நேரத்தில் இரண்டு அலைகள் 10 செக்கன் இடைவெளியில் வருகின்றன. இப்போது இவற்றை வைத்துப் பார்த்தால், முன் வந்த அலைகள் அலை நீளம் குறைந்தவை, அதான் வேகமாக வந்துவிட்டதே, பின் வந்த இரு அலைகளும் அலைநீளம் கூடியவை. மிகச் சுத்தமான உதாரணம் இல்லாவிடினும் உங்களுக்கு விளங்குவதற்காக கூறினேன்.

இதே போலதான் ஒவ்வொரு நிறத்திற்கும் அலைநீளம் உண்டு. அதில் மிகவும் அலைநீளம் கூடியது சிவப்பு (அலைநீளம் 620-750 நானோமீட்டர்). மிக மிக அலைநீளம் குறைந்தது ஊதா (அலைநீளம் 380-450 நானோமீட்டர்). இங்கு ஊதா ஒளியின் அலைநீளத்தை படிப்படியாக அதிகரிக்க, கருநீலம், நீலம், பச்சை, மஞ்சள், ஆரஞ்சு கடைசியாக சிவப்பு என்று இந்த எழு நிறங்களும் வரும்.

மின்காந்த அலைகளின் முழு அலைக்கற்றைத் தொகுதி. “VISIBLE” என்ற பகுதியில், வலப்பக்கத்தில் ஊதா நிறமும், இடப்பக்கத்தில் சிவப்பு நிறமும் இருப்பதை அவதானிக்க. அலைக்கற்றைக்கு கீழுள்ள பகுதியில், குறிப்பிட்ட மின்காந்த அலையில், அலைநீளத்தோடு ஒப்பிடக் கூடிய பொருட்களை குறித்திருக்கிறார்கள். (படத்தை கிளிக் செய்தது பெரிதாக்கி பாருங்கள்)

சரி, சிவப்பின் அலைநீளத்தை இன்னும் இழுத்து பெரிதாக்கினால் என்ன ஆகும்? அது இப்போது அகச்சிவப்பு (infrared) அலையாக மாறிவிடும். அதேபோல ஊதா ஒளியின் அலைநீளத்தை குறைத்தால் அது புறஊதாக் கதிர்களாக (ultraviolet) மாறிவிடும். இவை எல்லாமே மின்காந்த அலைவீச்சில் இருக்கும் கதிர்களே. ஆனால் எம்மால், சிவப்பில் இருந்து ஊதா வரையுள்ள அலைவீச்சை மட்டுமே கண்களால் பார்க்க முடியும். இது புலனாகும் நிறமாலை (visible spectrum) / புலனாகும் அலைவீச்சு என்று அழைக்கப்படும்.

இதெல்லாம் ஏன் சொல்கிறேன்? காரணம் உண்டு. இங்கு நாம் பார்க்கவேண்டிய விடயம் என்னவென்றால் இந்த நிகழ்வெல்லையனது அதனைச் சுற்றியுள்ள வெளியை மிகக்கடுமையாக இழுப்பதனால், வெளி விரிவடைகிறது, அதில் பயணிக்கும் ஒளியும் விரிவடைகிறது, அதாவது அதன் அலைநீளம் அதிகரிக்கிறது (அந்த ஸ்ப்ரிங் உதாரணத்தை நினைத்துக் கொள்ளுங்கள்). இப்படி விரிவடைந்து, விரிவடைந்து ஒரு கட்டத்தில் எல்லா நிறங்களும் சிவப்பு நிறத்தின் அலைநீளத்திற்கு வந்துவிடும். அதானால் தான் தொலைவில் இருந்து பார்ப்பவருக்கு நிகழ்வெல்லைக்குள் விழுந்துகொண்டிருக்கும் எதுவாயினும், சிவப்பாக தெரியும். ஆனாலும் இந்த சிவப்பு நிரந்தரம் இல்லை. நிகழ்வெல்லையை நெருங்க நெருங்க ஈர்ப்பு விசை அதிகரிப்பதால், சிவப்பின் அலை நீளமும் அதிகரிக்கும், ஒரு கட்டத்தில் அது புலனாகும் சிவப்பில் இருந்து விடுபட்டு, அகச்சிவப்பு கதிர்களாக மாறிவிடும் (அதைத் தொடர்ந்து படிப் படியாக அலைநீளம் அதிகரித்து மைக்ரோவேவ், ரேடியோவேவ் என்று செல்லும்), அதனை நம்மால் பார்க்க முடியாது. ஆக கருந்துளையின் நிகழ்வெல்லையை நோக்கி விழுபவர் கொஞ்சம் கொஞ்சமாக சிவப்பாக மாறி, பின் மங்கலாக சென்று ஒரு கட்டத்தில் நிகழ்வெல்லையை கடக்கும் போது மறைந்துவிடுவார். ஆனால் இதெல்லாம் தூரத்தில் இருந்து பார்ப்பவருக்குதான்.

கருந்துளையின் நிகழ்வெல்லையை நோக்கி செல்லுபவருக்கு இப்படி நிறங்கள் மாறுவது தெரியாது, ஏன் என்றால் அவரும் சேர்ந்துதான் வெளியோடு (space) சேர்ந்து இழுபடுகிறாரே!

இப்படி வெளியோடு சேர்ந்து இழுபடுவதில் இன்னுமொரு நிகழ்ச்சியை தூரத்தில் இருந்து அவதானிப்பவர் பார்க்கக்கூடும். அதாவது நீங்கள் (கருந்துளையை நோக்கி செல்பவர்) கருந்துளையை நோக்கி தரையிறங்குவது போல செல்கிறீர்கள் என்று வைத்துக் கொள்வோம். அப்படியென்றால் கால்கள் கருந்துளையை நோக்கியும், தலை கருந்துளைக்கு எதிர் திசையிலும் இருக்கும் என்று வைத்துக் கொள்வோம். இப்போது உங்கள் தலையை இழுப்பதை விட கால்களை கருந்துளையின் ஈர்ப்பு வேகமாக இழுக்கும், இப்படி தலைக்கும் காலுக்கும் வேறுபட்ட ஈர்ப்பு விசையானது, உங்களை அப்படியே நீட்டிவிடும், அதாவது சப்பாத்தி மாவை தயார் செய்து விட்டு, அந்த உருண்டைகளை இழுத்துப் பார்த்து இருகிறீர்களா, அப்படியே இழுபட்டுக் கொண்டே வருமே, அதேபோல நீங்களும் இழுபட்டுக்கொண்டே வந்து ஒரு கட்டத்தில் உங்கள் உடம்பில் உள்ள அணுக்கள் வரை இப்படி இழுபட்டு சிதைந்துவிடும்.

வெளியில் இருந்து பார்க்கும் ஒருவருக்கு, நாம் கருந்துளையின் நிகழ்வெல்லையை கடப்பதை பார்க்கவே முடியாது. எப்படி நிகழ்வெல்லை வெளியை இழுக்கிறதோ, அதேபோலே அது நேரத்தையும் அல்லவா இழுக்கிறது. இதப் பற்றி நாம் ஏற்கனவே தெளிவாக பார்த்துவிட்டோம், இருந்தும் இங்கு மீண்டும் சொல்வதற்கான காரணம், மீண்டும் ஒருமுறை புரியவைப்பதற்காகவே.

வெளியில் இருந்து பார்ப்பவருக்கு, நிகழ்வெல்லையை கடக்க முடிவிலி அளவு நேரம் ஆகும் போல தோன்றும். ஏன் என்றால் கருந்துளையின் நிகழ்வெல்லை வெளிநேரத்தை (space-time) மிக மிக அதிகமாக, கிட்டத்தட்ட முடிவிலி அளவிற்கு இழுத்து வளைத்துள்ளது. ஆனால் நிகழ்வெல்லையை கடப்பவருக்கு இந்தப் பிரச்சினை எல்லாம் இல்லை, அவர் சாதாரணமாக நிகழ்வெல்லையை கடந்துசென்றுவிடுவார்.

ஆனால் உள்ளே கடந்து சென்றுவிட்டால்த்தான் திரும்ப முடியாதே.

கருந்துளைக்குள் என்ன இருக்கும்? அதாவது நிகழ்வெல்லையின் உட்பகுதியில் என்ன இருக்கும் என்று பார்க்கலாம். அதற்கு முதல் ஒரு சிறிய எச்சரிக்கை. இனி நாம் பார்க்கபோகும் விடயங்கள், கணிதவியல் / இயற்பியல் துறையின் ஒரு எல்லையில் இருக்கும் கருத்துக்கள். இவை இன்னமும் பூரணமாக ஆராயப்படாத ஒன்று. நமக்குத் தெரிந்த இயற்பியல் / கணிதவியல் விதிகளைப் பயன்படுத்தி இப்படித்தான் இருக்கலாம் என்று கருதுகிறோம். எதிர்காலத்தில் இவற்றை வாய்ப்புப் பார்க்க சந்தர்பங்கள் அமையலாம்.

முற்றும் .